Reading and Working with Tabular Data

Overview

Teaching: 50 min
Exercises: 40 min

Questions

• What is a Pandas data frame?

• How do I get an overview on my tabular data?

• How do I read tabular data in different formats?

• How do I access subsets of a data frame?

• How do I calculate simple statistics like the mean?

Objectives

• Read data in various formats.

• Select individual values and subsections from data.

• Transform a data frame from messy to tidy data.

• Understand common data workflows (ETL) and strategies (split-apply-combine).

Read data

We use Pandas for reading, writing, and handling tabular data in Python as it is the de facto standard tool to do so.

Just as np is by convention the alias for numpy, so is pd for pandas.

import pandas as pd

We start by reading some data from a comma-separated values (CSV) file.

growth = pd.read_csv("data/yeast-growth.csv")

Inspect your data

Depending on your current Python environment a pandas.DataFrame object will automatically be displayed as text formatted to a table or as a prettier HTML table.

growth

    well  timepoint     od concentration_level  concentration
0      a          1  0.017                 low           0.01
1      b          1  0.017                 low           0.03
2      c          1  0.018              medium           1.00
3      d          1  0.017              medium           3.00
4      e          1  0.017              medium          30.00
..   ...        ...    ...                 ...            ...
450    c         65  0.228              medium           1.00
451    d         65  0.221              medium           3.00
452    e         65  0.065              medium          30.00
453    f         65  0.035                high         100.00
454    g         65  0.031                high         300.00

[455 rows x 5 columns]

By default, the output is configured to not show too many rows and columns. We can access more specific parts of a data frame using specific methods.

The beginning of a data frame can be accessed with the head method.

growth.head()

  well  timepoint     od concentration_level  concentration
0    a          1  0.017                 low           0.01
1    b          1  0.017                 low           0.03
2    c          1  0.018              medium           1.00
3    d          1  0.017              medium           3.00
4    e          1  0.017              medium          30.00

Correspondingly, the end of a data frame can be accessed with the tail method.

growth.tail()

    well  timepoint     od concentration_level  concentration
450    c         65  0.228              medium            1.0
451    d         65  0.221              medium            3.0
452    e         65  0.065              medium           30.0
453    f         65  0.035                high          100.0
454    g         65  0.031                high          300.0

You can also ask for a random number of rows. This is great for inspection since you have a chance to see rows from different parts of the data frame. It can also be convenient to develop an analysis with a subset of your data first because it will be faster (this matters if you work with tables that contain millions of rows).

growth.sample(10)

    well  timepoint     od concentration_level  concentration
332    d         48  0.120              medium           3.00
263    e         38  0.046              medium          30.00
139    g         20  0.032                high         300.00
376    f         54  0.036                high         100.00
415    c         60  0.231              medium           1.00
424    e         61  0.063              medium          30.00
392    a         57  0.234                 low           0.01
142    c         21  0.049              medium           1.00
312    e         45  0.051              medium          30.00
12     f          2  0.015                high         100.00

Notice the random indices.

Summaries

Looking at the actual values in your data is important to develop an understanding of them if you work with new data. However, in order to get an overview on your data, there are some useful summary methods.

If you just want to know the dimensions of your data frame, you can do so with the shape attribute.

growth.shape

(455, 5)

As you will see later on, it is sometimes necessary to look at the data types that pandas has inferred from your table.

growth.dtypes

well                    object
timepoint                int64
od                     float64
concentration_level     object
concentration          float64
dtype: object

The info method conveniently combines information on the shape and types in your data frame. In addition, it tells you about the index used and the memory consumption.

growth.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 455 entries, 0 to 454
Data columns (total 5 columns):
 #   Column               Non-Null Count  Dtype  
---  ------               --------------  -----  
 0   well                 455 non-null    object 
 1   timepoint            455 non-null    int64  
 2   od                   455 non-null    float64
 3   concentration_level  455 non-null    object 
 4   concentration        455 non-null    float64
dtypes: float64(2), int64(1), object(2)
memory usage: 17.9+ KB

Instead of summarizing the data frame object itself, you can get a high-level overview on the statistical distribution of your data.

growth.describe()

        timepoint          od  concentration
count  455.000000  455.000000     455.000000
mean    33.000000    0.077193      62.005714
std     18.782314    0.068110     102.928567
min      1.000000    0.015000       0.010000
25%     17.000000    0.032000       0.030000
50%     33.000000    0.042000       3.000000
75%     49.000000    0.099500     100.000000
max     65.000000    0.237000     300.000000

By default, this will only describe numeric columns. You can also get an overview on all columns including text and categorical columns (generally of type object).

growth.describe(include="all")

       well   timepoint          od concentration_level  concentration
count   455  455.000000  455.000000                 455     455.000000
unique    7         NaN         NaN                   3            NaN
top       a         NaN         NaN              medium            NaN
freq     65         NaN         NaN                 195            NaN
mean    NaN   33.000000    0.077193                 NaN      62.005714
std     NaN   18.782314    0.068110                 NaN     102.928567
min     NaN    1.000000    0.015000                 NaN       0.010000
25%     NaN   17.000000    0.032000                 NaN       0.030000
50%     NaN   33.000000    0.042000                 NaN       3.000000
75%     NaN   49.000000    0.099500                 NaN     100.000000
max     NaN   65.000000    0.237000                 NaN     300.000000

The NaN values displayed in the output are simply Pandas’ concept of missing values. Just pretend that they are empty cells.

Wording

I try to use data frame when talking about the object for computation and table when talking about data more generally; but I might mix them up as in my mind they are the same concept.

Tangent: Tidy Data

Hadley Wickham coined the concept of tidy data for statistics. What is tidy data?

You can also dive into the original publication from 2014 but it suffices to say that a tidy data structure is more intuitive for data visualization (plotting) and statistical analysis.

Reading files from different locales

Depending on what country’s standard your computer is set to (the ‘locale’), software such as Excel will use different characters to separate fields, for example, the default for a computer with the DK locale will be to use ; to separate fields and , to separate decimals. Try finding the right arguments to pandas.read_table to get something sensible out of "data/example-uk.txt" and "data/example-dk.txt". Use the inspection methods from before to see how pandas reads the data.

UK

Solution

uk_data = pd.read_table("data/example-uk.txt")
uk_data

      name;height;age;income
0       Ian;183;27;12,000.01
1     Peter;162;28;11,000.50
2  Bernhard;173;30;10,000.00
3    Steven;163;32;12,500.00

uk_data = pd.read_table("data/example-uk.txt", sep=";")
uk_data

       name  height  age     income
0       Ian     183   27  12,000.01
1     Peter     162   28  11,000.50
2  Bernhard     173   30  10,000.00
3    Steven     163   32  12,500.00

uk_data.dtypes

name      object
height     int64
age        int64
income    object
dtype: object

uk_data = pd.read_table("data/example-uk.txt", sep=";", thousands=",")
uk_data

       name  height  age    income
0       Ian     183   27  12000.01
1     Peter     162   28  11000.50
2  Bernhard     173   30  10000.00
3    Steven     163   32  12500.00

uk_data.dtypes

name       object
height      int64
age         int64
income    float64
dtype: object

DK

Solution

dk_data = pd.read_table("data/example-dk.txt")
dk_data

     name;height;age;income
0       Ian;183;27;12000,01
1     Peter;162;28;11100,50
2  Bernhard;173;30;11000,00
3    Steven;163;32;12500,00

dk_data = pd.read_table("data/example-dk.txt", sep=";")
dk_data

       name  height  age    income
0       Ian     183   27  12000,01
1     Peter     162   28  11100,50
2  Bernhard     173   30  11000,00
3    Steven     163   32  12500,00

dk_data.dtypes

name      object
height     int64
age        int64
income    object
dtype: object

dk_data = pd.read_table("data/example-dk.txt", sep=";", decimal=",")
dk_data

       name  height  age    income
0       Ian     183   27  12000.01
1     Peter     162   28  11100.50
2  Bernhard     173   30  11000.00
3    Steven     163   32  12500.00

dk_data.dtypes

name       object
height      int64
age         int64
income    float64
dtype: object

Other data formats

Excel

When you read data from spreadsheets (.xls, .xlsx, .ods), you do not need to worry about field separators or number formatting (but you need extra packages such as xlrd, openpyxl, or odfpy).

excel_data = pd.read_excel("data/example-dk.xlsx")
excel_data

       name  height  age    income
0       Ian     183   27  12000.01
1     Peter     162   28  11100.50
2  Bernhard     173   30  11000.00
3    Steven     163   32  12500.00

However, you may need to be careful with Excel’s interpretation of strings as dates (see Gene name errors are widespread in the scientific literature and Guidelines for human gene nomenclature) when loading tabular files in Excel.

Pandas will try to detect the right dependency for opening a spreadsheet.

date_data = pd.read_excel("data/example-datetime.ods")
date_data

        date      time
0 2020-03-02  03:34:23
1 2021-02-02  02:24:00
2 2021-09-01  16:01:22

Common date and time formats are automatically detected and converted to suitable Python data types.

date_data.dtypes

date    datetime64[ns]
time            object
dtype: object

You can conveniently combine multiple columns into one datetime object.

pd.read_excel("data/example-datetime.ods", parse_dates={"datetime": ["date", "time"]})

             datetime
0 2020-03-02 03:34:23
1 2021-02-02 02:24:00
2 2021-09-01 16:01:22

Further formats

There are many more formats that Pandas can read data from. Just type pd.read_ and press tab to see the list of auto-completion options. A few notable ones:

• All file-based read functions accept a remote URL as an option. We could have loaded the growth data with

pd.read_csv(
    "https://raw.githubusercontent.com/data-science-for-biotech/python-pandas-viz-ml/gh-pages/_episodes_rmd/data/yeast-growth.csv"
)

    well  timepoint     od concentration_level  concentration
0      a          1  0.017                 low           0.01
1      b          1  0.017                 low           0.03
2      c          1  0.018              medium           1.00
3      d          1  0.017              medium           3.00
4      e          1  0.017              medium          30.00
..   ...        ...    ...                 ...            ...
450    c         65  0.228              medium           1.00
451    d         65  0.221              medium           3.00
452    e         65  0.065              medium          30.00
453    f         65  0.035                high         100.00
454    g         65  0.031                high         300.00

[455 rows x 5 columns]

• In the context of the web, read_json can be very handy
• Tables are often stored in SQL databases, in that case read_sql is your friend

Accessing data

Let’s look at our old friend the growth data table again.

growth

    well  timepoint     od concentration_level  concentration
0      a          1  0.017                 low           0.01
1      b          1  0.017                 low           0.03
2      c          1  0.018              medium           1.00
3      d          1  0.017              medium           3.00
4      e          1  0.017              medium          30.00
..   ...        ...    ...                 ...            ...
450    c         65  0.228              medium           1.00
451    d         65  0.221              medium           3.00
452    e         65  0.065              medium          30.00
453    f         65  0.035                high         100.00
454    g         65  0.031                high         300.00

[455 rows x 5 columns]

By label

We can access individual columns (pandas.Series) by their names as string.

growth["od"]

0      0.017
1      0.017
2      0.018
3      0.017
4      0.017
       ...  
450    0.228
451    0.221
452    0.065
453    0.035
454    0.031
Name: od, Length: 455, dtype: float64

Notice how the display of series is different from data frames.

We can make powerful label based selections with the loc attribute.

growth.loc[:, "od"]

0      0.017
1      0.017
2      0.018
3      0.017
4      0.017
       ...  
450    0.228
451    0.221
452    0.065
453    0.035
454    0.031
Name: od, Length: 455, dtype: float64

Our data frames have two dimensions: the rows and columns. Here, we specify that we want all rows : and a single column "od". We can also select one or more columns as a list which will always return a data frame.

growth.loc[:, ["od"]]

        od
0    0.017
1    0.017
2    0.018
3    0.017
4    0.017
..     ...
450  0.228
451  0.221
452  0.065
453  0.035
454  0.031

[455 rows x 1 columns]

We use at to access an individual element with labels.

growth.at[451, "od"]

0.221

By index

We might be tempted to access a column by its index position directly.

growth[2]

Error in py_call_impl(callable, dots$args, dots$keywords): KeyError: 2

Detailed traceback:
  File "<string>", line 1, in <module>
  File "/home/moritz/.pyenv/versions/3.8.10/envs/biotech/lib/python3.8/site-packages/pandas/core/frame.py", line 3024, in __getitem__
    indexer = self.columns.get_loc(key)
  File "/home/moritz/.pyenv/versions/3.8.10/envs/biotech/lib/python3.8/site-packages/pandas/core/indexes/base.py", line 3082, in get_loc
    raise KeyError(key) from err

This does not work. Only labels are allowed here. Instead we use iloc for index location.

growth.iloc[:, 2]

0      0.017
1      0.017
2      0.018
3      0.017
4      0.017
       ...  
450    0.228
451    0.221
452    0.065
453    0.035
454    0.031
Name: od, Length: 455, dtype: float64

Again, we can select one or more columns as a data frame.

growth.iloc[:, [2]]

        od
0    0.017
1    0.017
2    0.018
3    0.017
4    0.017
..     ...
450  0.228
451  0.221
452  0.065
453  0.035
454  0.031

[455 rows x 1 columns]

We can also access individual elements.

growth.iat[451, 2]

0.221

By slices

We can also define label-based ranges over rows and columns.

growth.loc[:, "od":"concentration"]

        od concentration_level  concentration
0    0.017                 low           0.01
1    0.017                 low           0.03
2    0.018              medium           1.00
3    0.017              medium           3.00
4    0.017              medium          30.00
..     ...                 ...            ...
450  0.228              medium           1.00
451  0.221              medium           3.00
452  0.065              medium          30.00
453  0.035                high         100.00
454  0.031                high         300.00

[455 rows x 3 columns]

growth.loc[10:15, :]

   well  timepoint     od concentration_level  concentration
10    d          2  0.015              medium           3.00
11    e          2  0.019              medium          30.00
12    f          2  0.015                high         100.00
13    g          2  0.016                high         300.00
14    a          3  0.016                 low           0.01
15    b          3  0.015                 low           0.03

loc

Be careful that in label-based accession with loc, ranges are inclusive unlike numeric ranges in Python in general. Also be aware that since we have an integer index here, the label coincides with the index position.

growth.iloc[10:15, :]

   well  timepoint     od concentration_level  concentration
10    d          2  0.015              medium           3.00
11    e          2  0.019              medium          30.00
12    f          2  0.015                high         100.00
13    g          2  0.016                high         300.00
14    a          3  0.016                 low           0.01

N.B.: Index location ranges are exclusive.

By conditions

Pandas inherits from numpy the conditional selection of elements. These are essentially Boolean series or data frames known as masks.

growth[growth["od"] > 0.2]

    well  timepoint     od concentration_level  concentration
308    a         45  0.201                 low           0.01
315    a         46  0.208                 low           0.01
322    a         47  0.217                 low           0.01
329    a         48  0.227                 low           0.01
330    b         48  0.205                 low           0.03
336    a         49  0.229                 low           0.01
337    b         49  0.213                 low           0.03
343    a         50  0.232                 low           0.01
344    b         50  0.219                 low           0.03
350    a         51  0.233                 low           0.01
351    b         51  0.224                 low           0.03
357    a         52  0.237                 low           0.01
358    b         52  0.229                 low           0.03
364    a         53  0.236                 low           0.01
365    b         53  0.230                 low           0.03
366    c         53  0.207              medium           1.00
371    a         54  0.235                 low           0.01
372    b         54  0.231                 low           0.03
373    c         54  0.213              medium           1.00
378    a         55  0.237                 low           0.01
379    b         55  0.230                 low           0.03
380    c         55  0.218              medium           1.00
385    a         56  0.232                 low           0.01
386    b         56  0.231                 low           0.03
387    c         56  0.226              medium           1.00
392    a         57  0.234                 low           0.01
393    b         57  0.233                 low           0.03
394    c         57  0.230              medium           1.00
399    a         58  0.232                 low           0.01
400    b         58  0.228                 low           0.03
401    c         58  0.231              medium           1.00
406    a         59  0.230                 low           0.01
407    b         59  0.228                 low           0.03
408    c         59  0.230              medium           1.00
413    a         60  0.228                 low           0.01
414    b         60  0.225                 low           0.03
415    c         60  0.231              medium           1.00
420    a         61  0.227                 low           0.01
421    b         61  0.225                 low           0.03
422    c         61  0.230              medium           1.00
427    a         62  0.226                 low           0.01
428    b         62  0.222                 low           0.03
429    c         62  0.230              medium           1.00
430    d         62  0.205              medium           3.00
434    a         63  0.229                 low           0.01
435    b         63  0.225                 low           0.03
436    c         63  0.230              medium           1.00
437    d         63  0.212              medium           3.00
441    a         64  0.224                 low           0.01
442    b         64  0.221                 low           0.03
443    c         64  0.231              medium           1.00
444    d         64  0.217              medium           3.00
448    a         65  0.224                 low           0.01
449    b         65  0.220                 low           0.03
450    c         65  0.228              medium           1.00
451    d         65  0.221              medium           3.00

These masks can be combined using Boolean logic, making them very powerful tools for selecting just the right data.

growth[(growth["od"] > 0.2) & (growth["concentration_level"] == "medium")]

    well  timepoint     od concentration_level  concentration
366    c         53  0.207              medium            1.0
373    c         54  0.213              medium            1.0
380    c         55  0.218              medium            1.0
387    c         56  0.226              medium            1.0
394    c         57  0.230              medium            1.0
401    c         58  0.231              medium            1.0
408    c         59  0.230              medium            1.0
415    c         60  0.231              medium            1.0
422    c         61  0.230              medium            1.0
429    c         62  0.230              medium            1.0
430    d         62  0.205              medium            3.0
436    c         63  0.230              medium            1.0
437    d         63  0.212              medium            3.0
443    c         64  0.231              medium            1.0
444    d         64  0.217              medium            3.0
450    c         65  0.228              medium            1.0
451    d         65  0.221              medium            3.0

You can combine masks with loc to also sub-select columns.

growth.loc[(growth["od"] > 0.2) & (growth["concentration_level"] == "medium"), ["od", "timepoint"]]

        od  timepoint
366  0.207         53
373  0.213         54
380  0.218         55
387  0.226         56
394  0.230         57
401  0.231         58
408  0.230         59
415  0.231         60
422  0.230         61
429  0.230         62
430  0.205         62
436  0.230         63
437  0.212         63
443  0.231         64
444  0.217         64
450  0.228         65
451  0.221         65

Sometimes these conditions can be tedious to write, use the query method for a shorter form. Be careful, query uses Python’s condition logic, not numpy’s.

growth.query("od > 0.2 and concentration_level == 'medium'")

    well  timepoint     od concentration_level  concentration
366    c         53  0.207              medium            1.0
373    c         54  0.213              medium            1.0
380    c         55  0.218              medium            1.0
387    c         56  0.226              medium            1.0
394    c         57  0.230              medium            1.0
401    c         58  0.231              medium            1.0
408    c         59  0.230              medium            1.0
415    c         60  0.231              medium            1.0
422    c         61  0.230              medium            1.0
429    c         62  0.230              medium            1.0
430    d         62  0.205              medium            3.0
436    c         63  0.230              medium            1.0
437    d         63  0.212              medium            3.0
443    c         64  0.231              medium            1.0
444    d         64  0.217              medium            3.0
450    c         65  0.228              medium            1.0
451    d         65  0.221              medium            3.0

query is fancy enough to know how to use variables.

threshold = 0.2

growth.query("od > @threshold and concentration_level == 'medium'")

    well  timepoint     od concentration_level  concentration
366    c         53  0.207              medium            1.0
373    c         54  0.213              medium            1.0
380    c         55  0.218              medium            1.0
387    c         56  0.226              medium            1.0
394    c         57  0.230              medium            1.0
401    c         58  0.231              medium            1.0
408    c         59  0.230              medium            1.0
415    c         60  0.231              medium            1.0
422    c         61  0.230              medium            1.0
429    c         62  0.230              medium            1.0
430    d         62  0.205              medium            3.0
436    c         63  0.230              medium            1.0
437    d         63  0.212              medium            3.0
443    c         64  0.231              medium            1.0
444    d         64  0.217              medium            3.0
450    c         65  0.228              medium            1.0
451    d         65  0.221              medium            3.0

Views

Selecting a subset of your data frame by any of the previous means creates a view on that part of the data frame. This is faster since the data is not copied and lets you change elements in a part of the table. Be careful that this may lead to unintended consequences.

growth.loc[0:5, :] = None

growth.head(10)

   well  timepoint     od concentration_level  concentration
0  None        NaN    NaN                None            NaN
1  None        NaN    NaN                None            NaN
2  None        NaN    NaN                None            NaN
3  None        NaN    NaN                None            NaN
4  None        NaN    NaN                None            NaN
5  None        NaN    NaN                None            NaN
6     g        1.0  0.015                high         300.00
7     a        2.0  0.015                 low           0.01
8     b        2.0  0.018                 low           0.03
9     c        2.0  0.021              medium           1.00

A comprehensive tutorial can be found in the Pandas documentation.

Working with data

Just like numpy, Pandas offers basic statistical methods out-of-the-box. We can apply them to single columns,

growth["od"].min()

0.015

multiple columns,

growth[["od", "concentration"]].max()

od                 0.237
concentration    300.000
dtype: float64

or even rows.

growth[["od", "concentration"]].mean(axis=1)

0           NaN
1           NaN
2           NaN
3           NaN
4           NaN
         ...   
450      0.6140
451      1.6105
452     15.0325
453     50.0175
454    150.0155
Length: 455, dtype: float64

growth[["od", "concentration"]].std(axis=1)

0             NaN
1             NaN
2             NaN
3             NaN
4             NaN
          ...    
450      0.545886
451      1.965050
452     21.167241
453     70.685929
454    212.110114
Length: 455, dtype: float64

Split-apply-combine

Another powerful operation and a very common strategy for data transformation is split, apply, combine. This pattern is provided by pandas in the form of the groupby method.

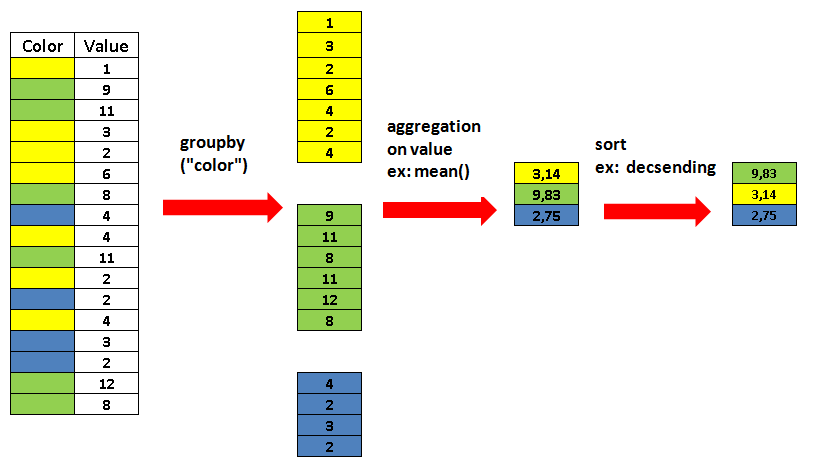
growth.groupby("well")[["od", "concentration"]].mean()

            od  concentration
well                         
a     0.123500           0.01
b     0.117969           0.03
c     0.109375           1.00
d     0.088328           3.00
e     0.043891          30.00
f     0.033937         100.00
g     0.029738         300.00

Cleaning messy data

Can you transform this messy table into a tidy one? You may need the melt function to change the table layout.

messy = pd.read_csv("data/yeast-growth-messy.csv")

Solution

messy

      V1      V2      V3     V4     V5     V6  ...    V63    V64    V65    V66    V67    V68
0  Test1     low    0.01  0.017  0.015  0.016  ...  0.228  0.227  0.226  0.229  0.224  0.224
1  Test1     low    0.03  0.017  0.018  0.015  ...  0.225  0.225  0.222  0.225  0.221  0.220
2  Test1  medium    1.00  0.018  0.021  0.016  ...  0.231  0.230  0.230  0.230  0.231  0.228
3  Test1  medium    3.00  0.017  0.015  0.017  ...  0.190  0.196  0.205  0.212  0.217  0.221
4  Test1  medium   30.00  0.017  0.019  0.016  ...  0.062  0.063  0.062  0.063  0.063  0.065
5  Test1    high  100.00  0.016  0.015  0.015  ...  0.037  0.035  0.035  0.034  0.035  0.035
6  Test1    high  300.00  0.015  0.016  0.015  ...  0.031  0.032  0.031  0.031  0.030  0.031

[7 rows x 68 columns]

messy.columns

Index(['V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11',
       'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21',
       'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'V29', 'V30', 'V31',
       'V32', 'V33', 'V34', 'V35', 'V36', 'V37', 'V38', 'V39', 'V40', 'V41',
       'V42', 'V43', 'V44', 'V45', 'V46', 'V47', 'V48', 'V49', 'V50', 'V51',
       'V52', 'V53', 'V54', 'V55', 'V56', 'V57', 'V58', 'V59', 'V60', 'V61',
       'V62', 'V63', 'V64', 'V65', 'V66', 'V67', 'V68'],
      dtype='object')

del messy["V1"]

from string import ascii_lowercase

messy["well"] = list(ascii_lowercase[:len(messy)])

long_data = pd.melt(messy, id_vars=["V2", "V3", "well"])
long_data

         V2      V3 well variable  value
0       low    0.01    a       V4  0.017
1       low    0.03    b       V4  0.017
2    medium    1.00    c       V4  0.018
3    medium    3.00    d       V4  0.017
4    medium   30.00    e       V4  0.017
..      ...     ...  ...      ...    ...
450  medium    1.00    c      V68  0.228
451  medium    3.00    d      V68  0.221
452  medium   30.00    e      V68  0.065
453    high  100.00    f      V68  0.035
454    high  300.00    g      V68  0.031

[455 rows x 5 columns]

long_data["variable"].replace(dict(zip(long_data["variable"].unique(), range(1, len(long_data["variable"].unique()) + 1))), inplace=True)

long_data.rename(columns={"V2": "concentration_level", "V3": "concentration", "variable": "timepoint"}, inplace=True)

long_data

    concentration_level  concentration well  timepoint  value
0                   low           0.01    a          1  0.017
1                   low           0.03    b          1  0.017
2                medium           1.00    c          1  0.018
3                medium           3.00    d          1  0.017
4                medium          30.00    e          1  0.017
..                  ...            ...  ...        ...    ...
450              medium           1.00    c         65  0.228
451              medium           3.00    d         65  0.221
452              medium          30.00    e         65  0.065
453                high         100.00    f         65  0.035
454                high         300.00    g         65  0.031

[455 rows x 5 columns]

Tangent: Extract, Transform, Load (ETL)

The process we have just seen is known as extract, transform, load or simply ETL. It describes the ubiquitous data workflow of reading data (extract with, for example, pd.read_csv), cleaning up the data (transform) as we have done with the messy growth curves above, and storing the tidy data again for subsequent use (load with, for example, to_excel).

Outlook

• Tidy pandas data frames are excellent structures for visualizing data, either with the built-in methods or other packages. This will be part of the next episode.
• The package statsmodels can be used to fit statistical models to tidy data frames in a convenient fashion using R-style formulas.
• Data frames due to their column names are more descriptive than pure numeric matrices (numpy.ndarray) which is handy in many tasks, for example, in machine learning as shown in the last episode.

Key Points

• Use pandas.read_* and pandas.DataFrame.to_* to import / export data.

• The method info describes the data frame object.

• The method describe summarizes value distributions in columns.

• You can use labels or index locations to select both subsets and elements from your data frame.

• Selection using conditions is very powerful.

• Selections create views on your original data.

• Use mean, max, min, and others to calculate simple statistics.

• Use split-apply-combine to calculate statistics within groups in a data frame.

Morning Break

Overview

Teaching: 0 min
Exercises: 0 min

Questions

Objectives

Key Points

Visualize Your Data

Overview

Teaching: 45 min
Exercises: 30 min

Questions

• What tools exist to plot data in Python?

• How do I make a basic plot?

• What visuals are available?

• How can I best visualize groups of data?

Objectives

• Get an introduction to Pandas plotting.

• Get a high-level overview on plotting in Python.

• Learn about the grammar of graphics.

• Learn to apply the grammar of graphics through altair.

• Learn how to group data.

• Learn how to use facets.

• Develop an understanding of the rich visualization diversity that exists.

Native Pandas plotting

import pandas as pd

Let’s work with the familiar growth data from last episode.

growth = pd.read_csv("data/yeast-growth.csv")

Pandas provides a few quick plotting methods. It uses matplotlib under the hood to generate graphics.

import matplotlib.pyplot as plt

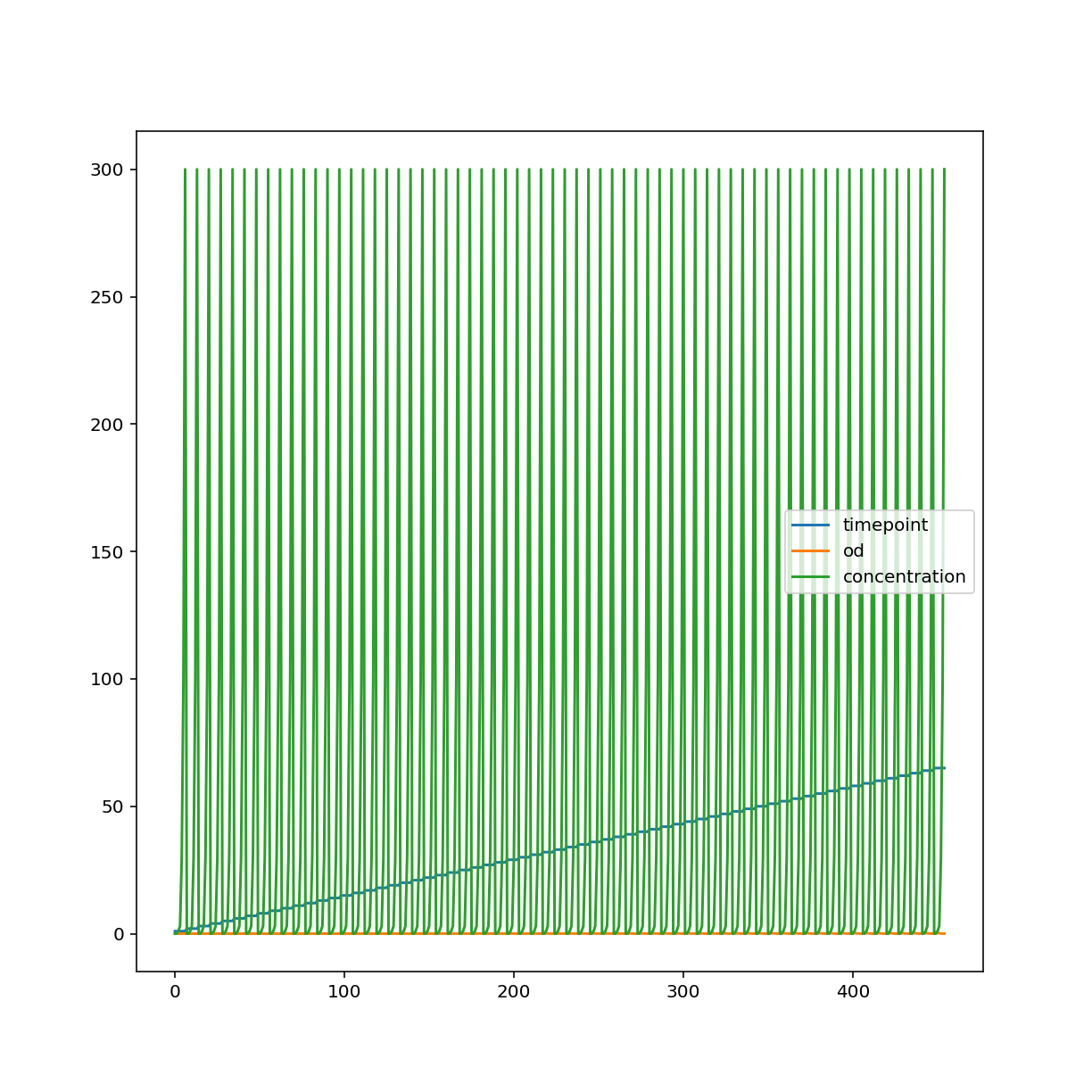
The default plot method draws lines for every numeric column in the data frame using the index as the horizontal axis.

growth.plot()

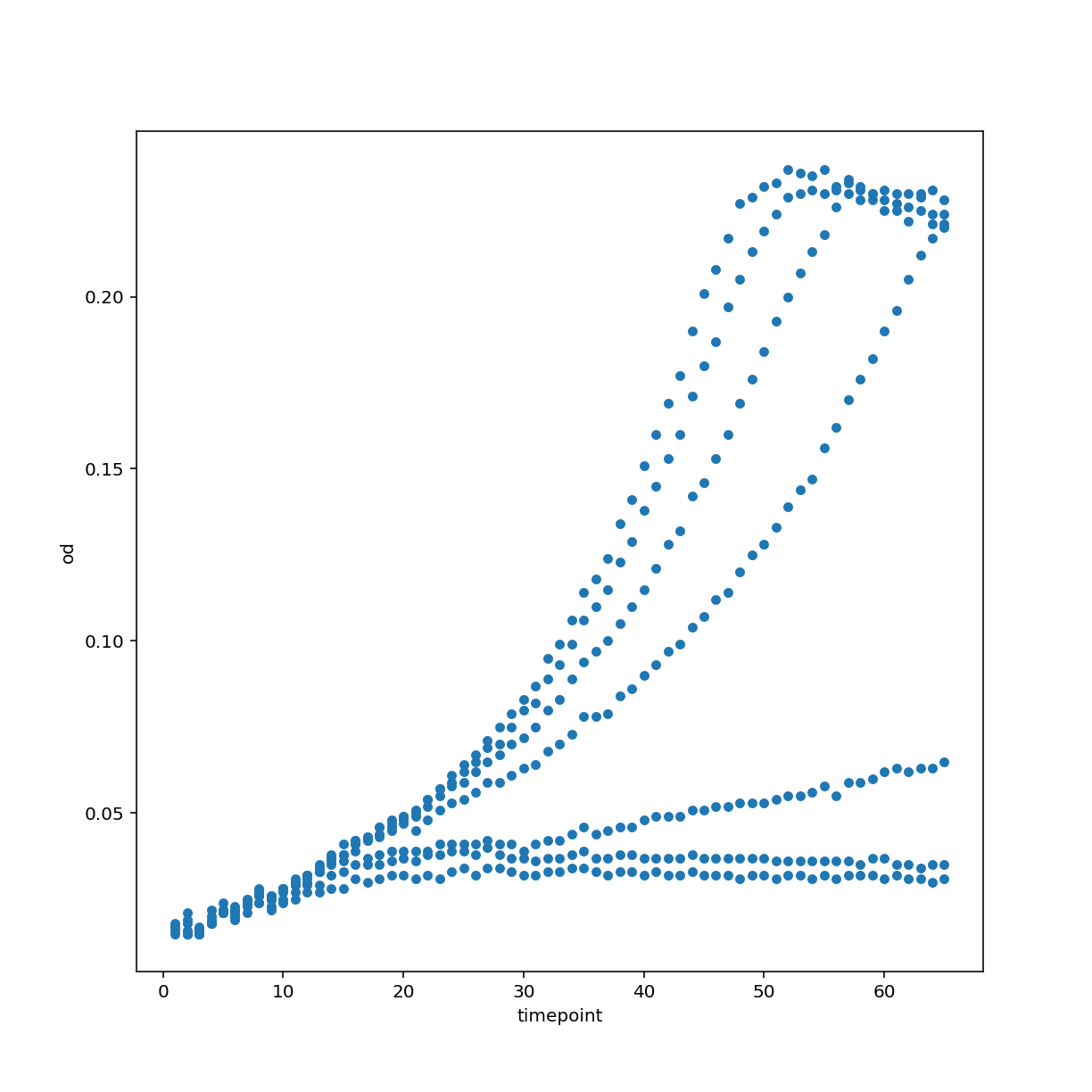
We can specify a different kind of plot, choosing columns explicitly.

growth.plot.scatter("timepoint", "od")

Other types of plots include a histogram. You can also see that we use matplotlib directly in order to customize the plot further.

growth["concentration"].plot.hist(bins=30)

<AxesSubplot:ylabel='Frequency'>

plt.xlabel("concentration")

Text(0.5, 0, 'concentration')

plt.show()

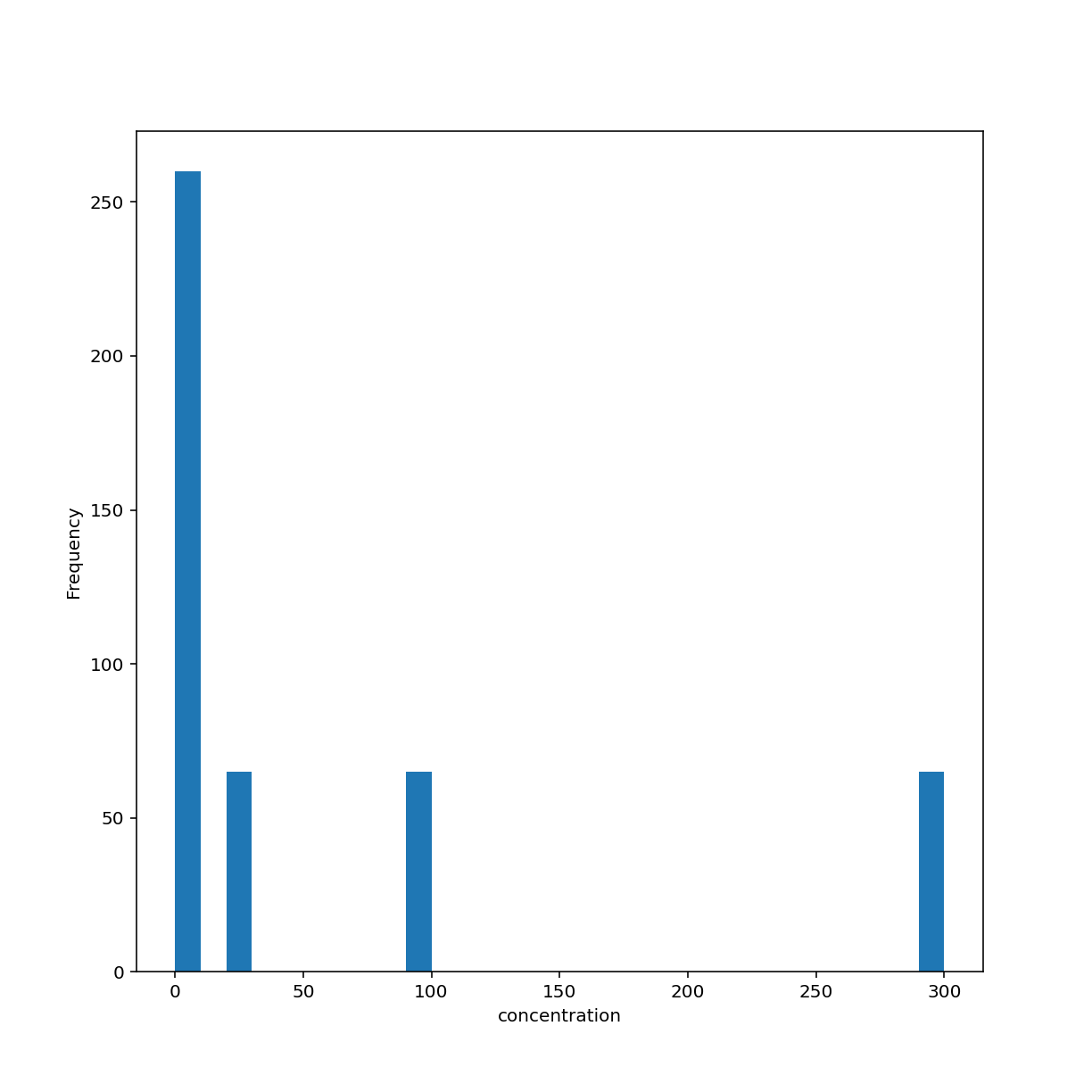
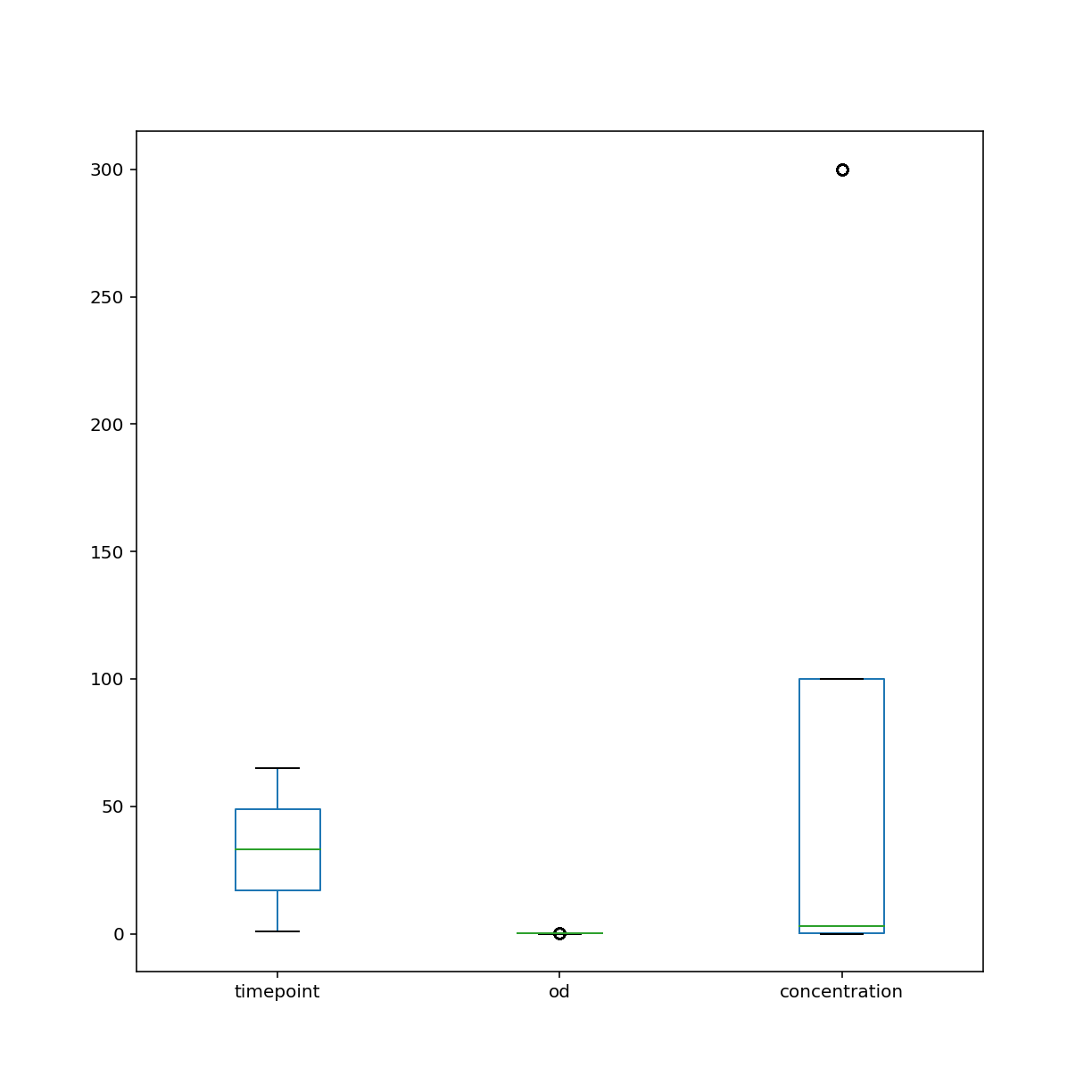
Another type of plot for showing distributions is the box plot which, again, by default uses numeric columns.

growth.plot.box()

My opinion on native Pandas plotting:

• Great for quick visualization
• Unlike base matplotlib, can refer to data by column name
• Selecting data using Pandas indexing is awesome
• Customizing figures with matplotlib commands can be tedious
• Adding trend lines, regression plots, managing colors can become a pain in the neck

State of plotting in Python

https://pyviz.org/overviews/index.html

• Overwhelming number of options
• Why we chose altair for this workshop:
  • It based on Vega-Lite’s visualization grammar
  • Vega in turn is based on D3.js thus it natively works in your browser and provides interactivity
  • Main authors Jake Vanderplas and Brian Granger are well known figures in the Python visualization space and as academics can be expected to keep maintaining the project

Grammar of Graphics

The grammar of graphics was described by Leland Wilkinson. It was later updated by Hadley Wickham with ideas developed during the creation of his famous R plotting software ggplot2. This blog has a decent summary of both. In lose terms, the idea is that every visualization has the following ingredients:

• data (ideally in a tidy format)
• a coordinate system to draw in the data
• visual marks (geometries) that represent the data
• aesthetics that describe which data encode visual properties

This all sounds a bit abstract. Let’s dive into examples.

Introduction to altair

We need the altair package, of course.

import altair as alt
width = 800
height = 600

Here we create an altair Chart object with our tidy growth data frame. The default coordinate system is Cartesian with two axes. We encode our data and specify that the time points should describe our x-axis coordinate and optical density the y-axis coordinate. Finally, we want this two-dimensional data to be displayed by the visual mark points.

The default output size is a bit small in my opinion so we configure it to be a bit larger.

alt.Chart(growth).encode(
    x="timepoint", y="od"
).mark_point().configure_view(continuousWidth=width, continuousHeight=height)

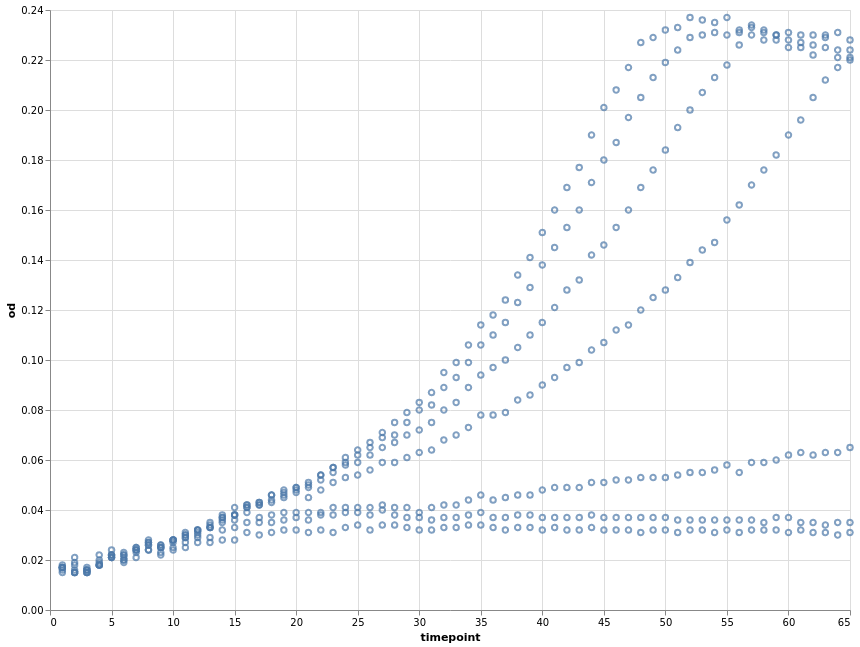
We can, at any point, store our current chart specification in a variable and later apply further specifications to it.

base = alt.Chart(growth).encode(x="timepoint", y="od")

How about using lines as the visual mark?

base.mark_line().configure_view(continuousWidth=width, continuousHeight=height)

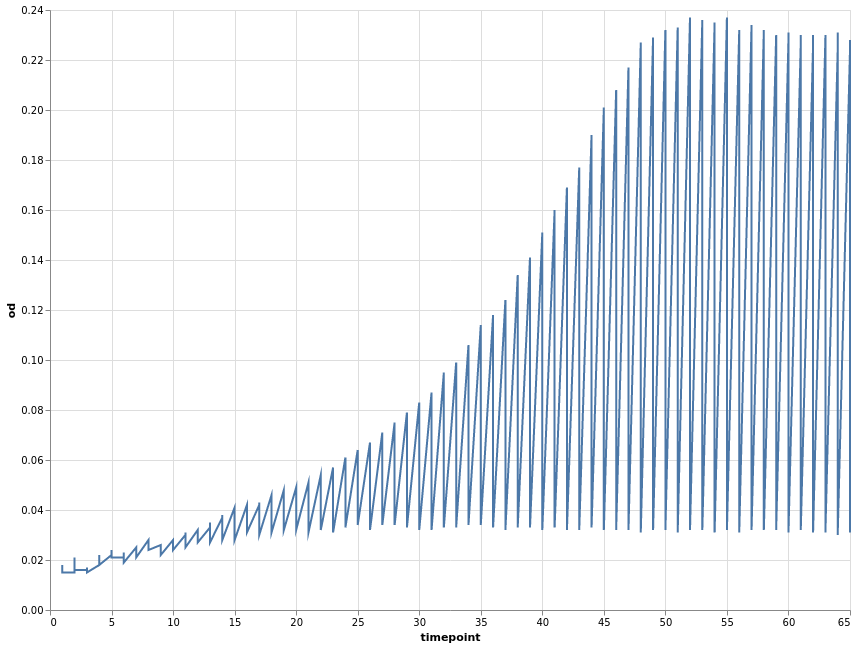
The above plot has the same problems as the Pandas default plot. Our data was recorded per well. We can use this variable to encode a third dimension that groups our data. Common options are colour or shape/linetype.

base.encode(color="well").mark_line(point=True).configure_view(
    continuousWidth=width, continuousHeight=height
)

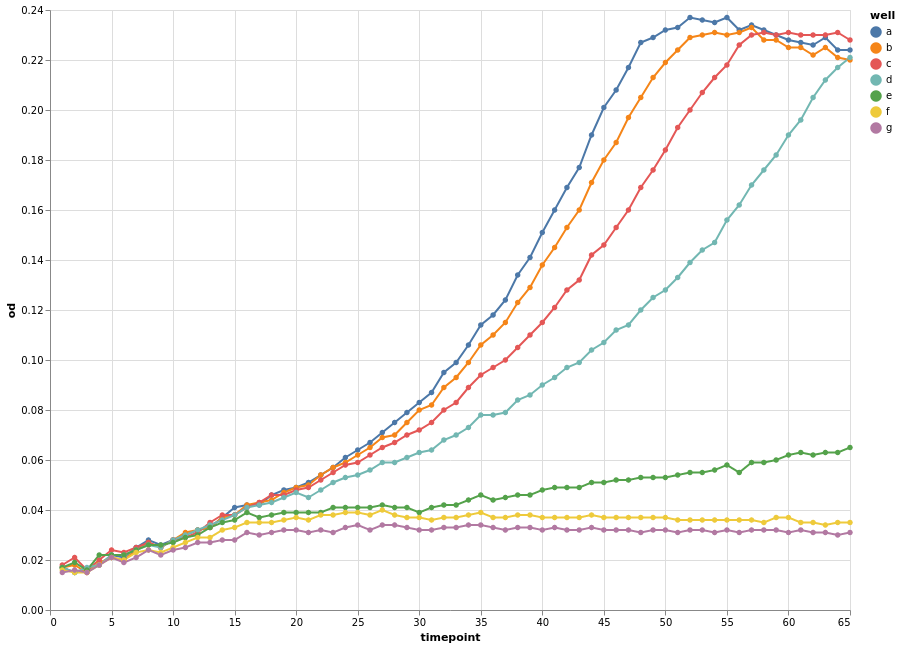
This looks much better already. We also changed the visual mark to be a point and line.

Instead of defining separate groups for each growth time course, we can separate each individual time course into its own plot. This is known as facetting. Using facets can be handy but information is more spread out. Comparing different time courses is harder in this format.

base.mark_line(point=True).facet("well", columns=3)

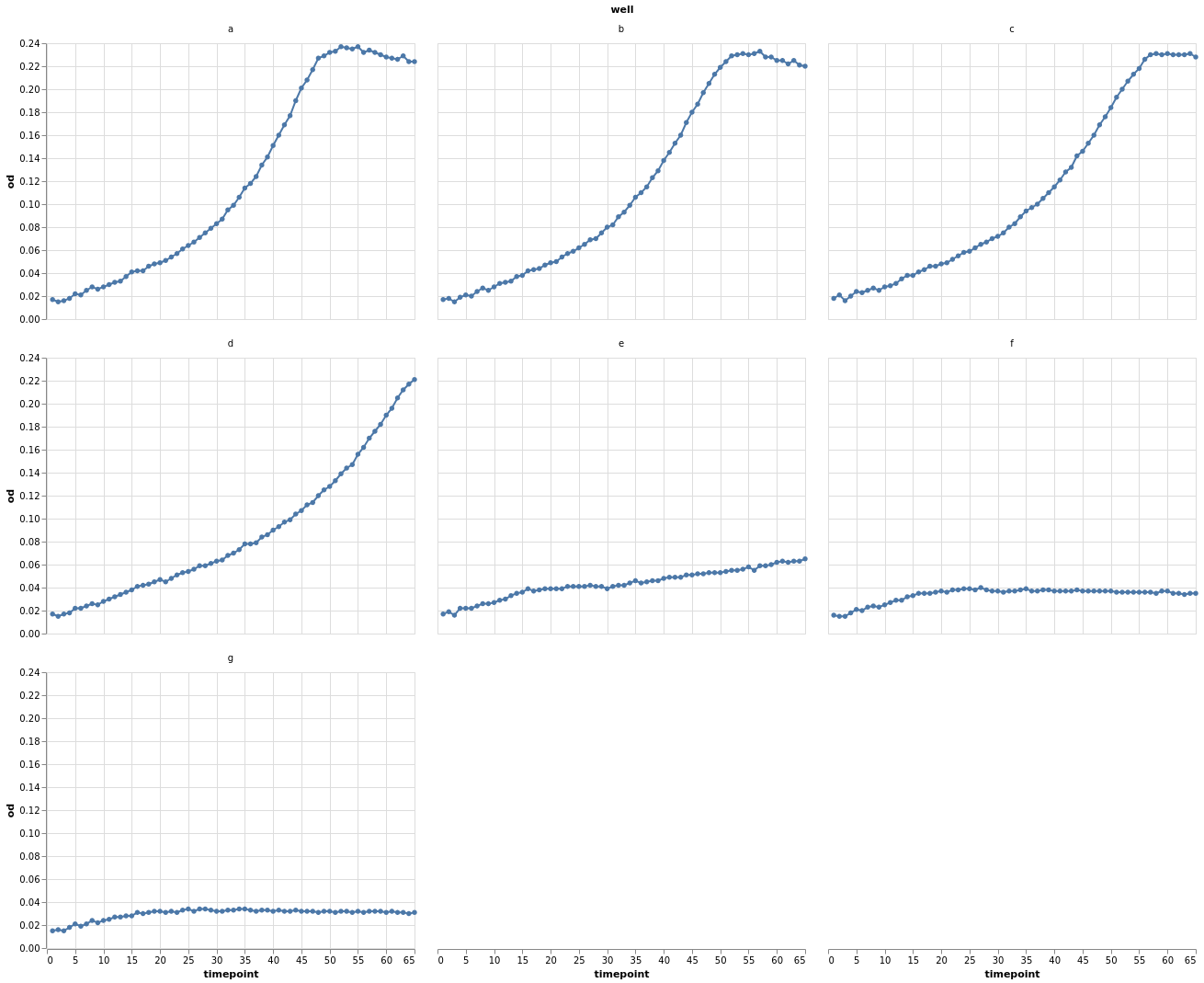
Let’s look again at the individual data points grouped by well.

chart = alt.Chart(growth).encode(x="timepoint", y="od", color="well").mark_point()
chart.configure_view(continuousWidth=width, continuousHeight=height)

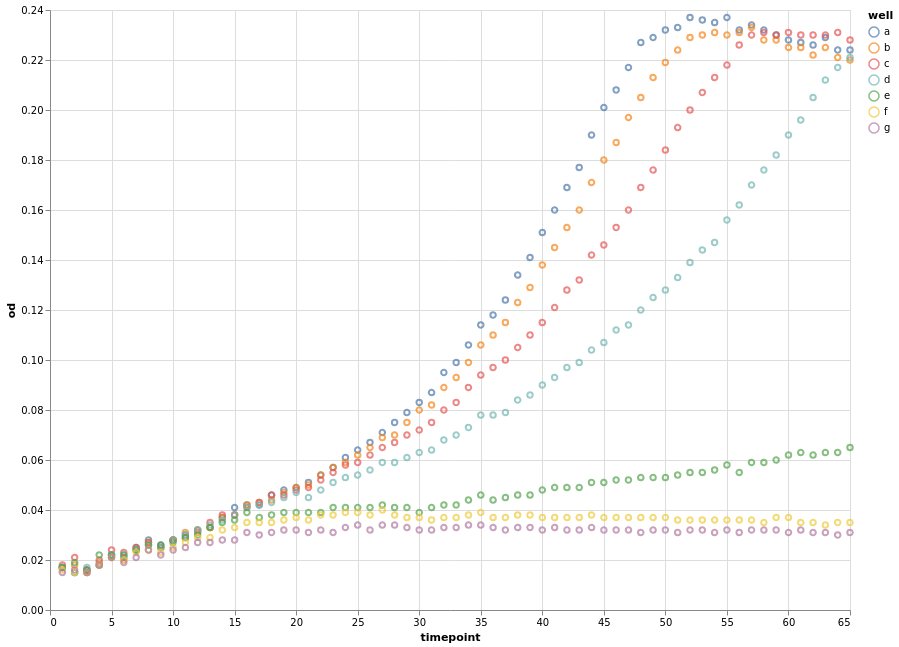
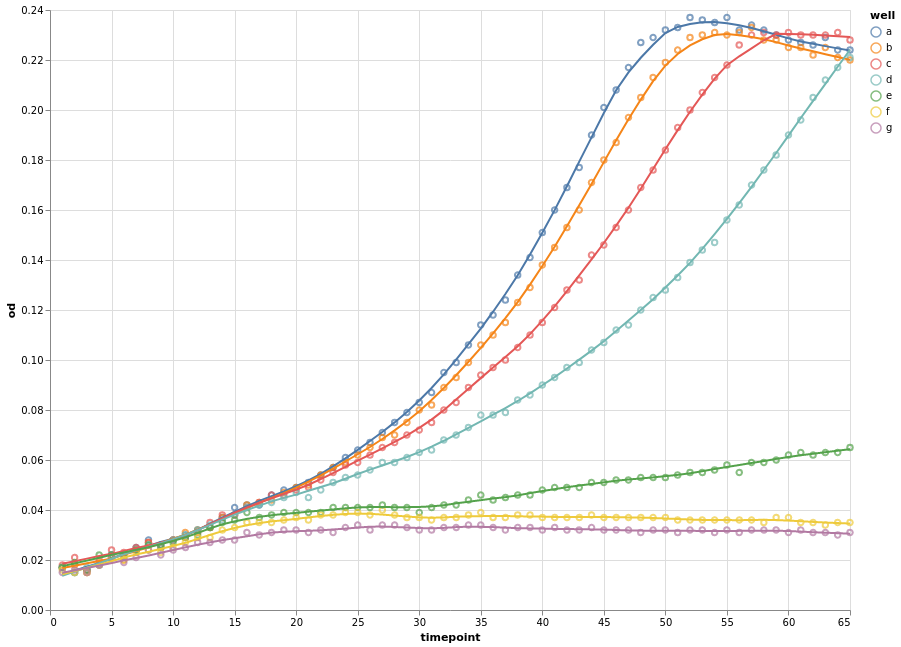
Instead of connecting each consecutive data point with a straight line, we can apply a smoothing data transformation. In the following example, we use a locally estimated scatterplot smoothing (LOESS) transformation.

(
    chart
    + chart.transform_loess(
        "timepoint", "od", groupby=["well"], bandwidth=0.15
    ).mark_line()
).configure_view(continuousWidth=width, continuousHeight=height)

We can now combine the concepts that we have learnt to introduce a fourth dimension, the measured concentration. Since the concentration is a measured quantity, we use a continuous colour scale to represent it. We still group our data by wells and apply smoothing. As an example, we vary the point shape.

Please not that for the first time we explicitly encode the type of the variables. Q means quantitative (continuous) and N means nominal (categorical).

fancy_chart = alt.Chart(growth).encode(
    x="timepoint:Q",
    y="od:Q",
    detail="well:N",
    color=alt.Color("concentration:Q", scale=alt.Scale(type="log", scheme="greenblue")),
)
(
    fancy_chart.transform_loess(
        "timepoint", "od", groupby=["well", "concentration"], bandwidth=0.1
    ).mark_line()
    + fancy_chart.encode(shape="well:N").mark_point()
).configure_view(continuousWidth=width, continuousHeight=height)

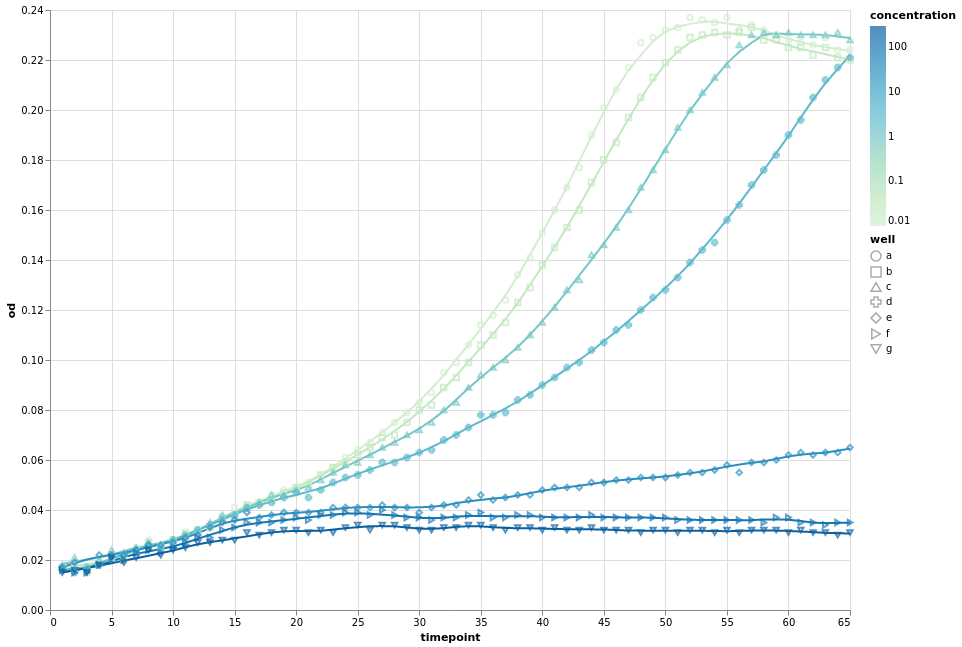
Other visual marks

Naturally, altair offers more than just lines and points.

An interactive histogram:

brush = alt.selection_interval(encodings=["x"])

base = (
    alt.Chart(growth).mark_bar().encode(y="count():Q").properties(width=600, height=100)
)

alt.vconcat(
    base.encode(
        alt.X(
            "od:Q", bin=alt.Bin(maxbins=30, extent=brush), scale=alt.Scale(domain=brush)
        )
    ),
    base.encode(
        alt.X("od:Q", bin=alt.Bin(maxbins=30)),
    ).add_selection(brush),
)

Or how about boxplot of optical density per well.

alt.Chart(growth).mark_boxplot().encode(x="well:O", y="od:Q").configure_view(continuousWidth=width, continuousHeight=height)

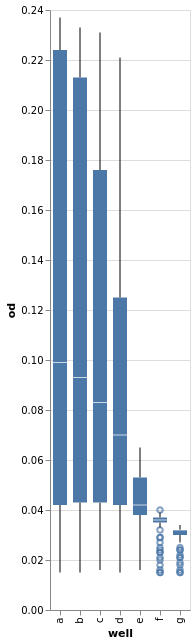
Many more examples exist.

Key Points

• Pandas provides quick ways to create simple visualizations.

• A layered grammar of graphics implementation provides a structured approach to plotting.

• A good implementation can make expressing complex visualizations straightforward.

Lunch Break

Overview

Teaching: 0 min
Exercises: 0 min

Questions

Objectives

Key Points

Machine Learning

Overview

Teaching: 70 min
Exercises: 20 min

Questions

• What is machine learning?

• What kind of tasks can I apply machine learning to?

• How do I perform machine learning with scikit-learn?

• How do I interpret my results?

Objectives

• Get a rough overview on machine learning.

• Clean up a real world data set.

• Get an introduction scikit-learn.

• Apply dimensionality reduction, clustering, classification, and anomaly detection.

• Visualize results in diverse ways.

Episode Credit

This episode is adapted and enhanced from https://github.com/YaleDHLab/lab-workshops/tree/master/machine-learning.

As a real-world dataset for practicing machine learning tasks on, we will use relative abundances of gut microbiota. In a brand new publication

Wibowo, Marsha C., Zhen Yang, Maxime Borry, Alexander Hübner, Kun D. Huang, Braden T. Tierney, Samuel Zimmerman, et al. 2021. “Reconstruction of Ancient Microbial Genomes from the Human Gut.” Nature, May. https://doi.org/10.1038/s41586-021-03532-0.

modern industrial and pre-industrial fecal microbiota were compared to some ancient samples (palaeofaeces).

ETL relative microbial abundances

import pandas as pd

While the following command is running, take a look at the spreadsheet itself.

raw = pd.read_excel(
    "data/41586_2021_3532_MOESM6_ESM.xlsx",
    sheet_name="Tab1-MetaPhlAn2_output",
    header=None,
)

What did we extract from the spreadsheet?

raw.head(10)

                                                 0           1    ...       799       800
0                                                NaN  Paleofeces  ...      Soil      Soil
1                                                NaN      UT43.2  ...  1043.4.1  3567.1.1
2                                         k__Archaea     7.18607  ...         0    0.0049
3                        k__Archaea|p__Euryarchaeota     7.18607  ...         0    0.0049
4        k__Archaea|p__Euryarchaeota|c__Archaeoglobi           0  ...         0         0
5  k__Archaea|p__Euryarchaeota|c__Archaeoglobi|o_...           0  ...         0         0
6  k__Archaea|p__Euryarchaeota|c__Archaeoglobi|o_...           0  ...         0         0
7  k__Archaea|p__Euryarchaeota|c__Archaeoglobi|o_...           0  ...         0         0
8        k__Archaea|p__Euryarchaeota|c__Halobacteria           0  ...         0         0
9  k__Archaea|p__Euryarchaeota|c__Halobacteria|o_...           0  ...         0         0

[10 rows x 801 columns]

This is the output from a particular software (MetaPhlAn2) for estimating microbial abundances from metagenomic sequencing (MGS) data. The single letter with double underscore prefix in the first column denotes the taxonomic rank. Multiple ranks are divided by | and describe a lineage.

The first two rows in the table describe the type of sample and a sample identifier.

raw.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3636 entries, 0 to 3635
Columns: 801 entries, 0 to 800
dtypes: object(801)
memory usage: 22.2+ MB

Due to the sample identifiers in every column, they are all of type object rather than numerical.

Let’s make this tidy!

Tidying up

Sample meta information

We will split the information that describes the samples. We will also get to know another Pandas feature, the pipe which allows us to chain function calls. In order to make full use of the chaining, we also need a function to assign values to the data frame.

def set_element(df, row_idx, col_idx, value):
    result = df.copy()
    result.iat[row_idx, col_idx] = value
    return result

Our meta information is in the first two rows. We then set meaningful names in the currently empty fields. Next we set the first column as the row index. Then we transpose the table such that our two rows become two columns and reset the index of that transposed data frame such that we end up with a range index starting at zero.

observations = (
    raw.iloc[:2, :]
    .pipe(set_element, 0, 0, "label")
    .pipe(set_element, 1, 0, "sample")
    .set_index(0)
    .T.reset_index(drop=True)
)

The result looks as follows:

observations.head(10)

0           label   sample
0      Paleofeces   UT43.2
1      Paleofeces    AW107
2      Paleofeces    AW108
3      Paleofeces   AW110A
4      Paleofeces    Zape1
5      Paleofeces    Zape2
6      Paleofeces    Zape3
7      Paleofeces   UT30.3
8  Non-industrial  MEX3158
9  Non-industrial  MEX3160

Inspect the observations

Can you confirm that we haven’t lost any samples? Additionally, is there something interesting to be said about the data?

Solution

observations.shape

(800, 2)

The observations have the same dimension as the relative abundances.

observations.describe()

0            label      sample
count          800         800
unique           4         800
top     Industrial  A34_02_1FE
freq           418           1

We see that there are four unique labels and that the label ‘Industrial’ is the most common.

observations["label"].value_counts()

Industrial        418
Non-industrial    371
Paleofeces          8
Soil                3
Name: label, dtype: int64

An overview on the number of samples per label.

Now that we have the sample meta information in a tidy format, it is time that we clean up the relative abundances.

Relative abundances

There is a lot of information contained in the first column. Let’s split this information into multiple columns. The taxonomic rank deserves its own column so that we can later filter on it. For convenience, we also keep the kingdom of every sample for later data filtering.

Our strategy is then:

• Split the strings in the first column on |
• The first element in the resulting list is the highest taxonomic rank, i.e., kingdom
• The last element in the list is the lowest taxonomic rank, this will be anything from kingdom down to strain level
• We remove the rank prefix to end up with nice names

def transform_taxonomic_rank(df):
    result = df.rename(columns={0: "taxonomy"})
    lineage = result["taxonomy"].str.split("|")
    result["kingdom"] = (
        lineage.map(lambda element: element[0])
        .str.split("__", n=1, expand=True)
        .iloc[:, -1]
    )
    result[["rank", "taxonomy"]] = lineage.map(lambda element: element[-1]).str.split(
        "__", n=1, expand=True
    )
    return result

transformed = transform_taxonomic_rank(raw.iloc[2:, :])

Let’s see what our result looks like.

Inspect the transformed data frame

Briefly investigate the transformed data frame.

Solution

transformed.head(10)

                         taxonomy        1        2        3  ... 799     800  kingdom rank
2                         Archaea  7.18607  3.52607  0.10627  ...   0  0.0049  Archaea    k
3                   Euryarchaeota  7.18607  3.52607  0.10627  ...   0  0.0049  Archaea    p
4                    Archaeoglobi        0        0        0  ...   0       0  Archaea    c
5                 Archaeoglobales        0        0        0  ...   0       0  Archaea    o
6                Archaeoglobaceae        0        0        0  ...   0       0  Archaea    f
7   Archaeoglobaceae_unclassified        0        0        0  ...   0       0  Archaea    g
8                    Halobacteria        0        0        0  ...   0       0  Archaea    c
9                 Halobacteriales        0        0        0  ...   0       0  Archaea    o
10               Halobacteriaceae        0        0        0  ...   0       0  Archaea    f
11                  Halobacterium        0        0        0  ...   0       0  Archaea    g

[10 rows x 803 columns]

transformed.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3634 entries, 2 to 3635
Columns: 803 entries, taxonomy to rank
dtypes: object(803)
memory usage: 22.3+ MB

transformed.describe()

              taxonomy       1       2       3  ...     799     800   kingdom  rank
count             3633  3634.0  3634.0  3634.0  ...  3634.0  3634.0      3633  3634
unique            3527   150.0   134.0   132.0  ...   123.0   292.0         4     9
top     Viruses_noname     0.0     0.0     0.0  ...     0.0     0.0  Bacteria     s
freq                 5  3312.0  3349.0  3342.0  ...  3399.0  3056.0      3020  1459

[4 rows x 803 columns]

transformed["kingdom"].value_counts()

Bacteria     3020
Viruses       479
Eukaryota      91
Archaea        43
Name: kingdom, dtype: int64

transformed["rank"].value_counts()

s               1459
t               1267
g                503
f                216
o                 98
c                 58
p                 28
k                  4
unclassified       1
Name: rank, dtype: int64

From our inspection of the data, we decide that it’s best to remove the abundance of unclassified sequencing reads. In addition, I don’t trust the read assignment to virus genomes and they don’t play a large role. We remove those as well.

Similarly to before, we then set the new columns as the row index, then we convert all abundances from object types to float types, transpose the data frame, and reset the index again for a nice range starting from zero.

abundance = (
    transformed.query("kingdom != 'Viruses' and rank != 'unclassified'")
    .set_index(["kingdom", "rank", "taxonomy"])
    .astype(float)
    .T.reset_index(drop=True)
)

We have chosen three columns as the index here. That means, we are creating an index with multiple levels (a pandas.MultiIndex). Multi indeces can be tricky to work with. We will just use them here but do not expect a full understanding.

abundance.head(10)

kingdom   Archaea                ...               Eukaryota              
rank            k             p  ...                       s             t
taxonomy  Archaea Euryarchaeota  ... Enterocytozoon_bieneusi GCA_000209485
0         7.18607       7.18607  ...                     0.0           0.0
1         3.52607       3.52607  ...                     0.0           0.0
2         0.10627       0.10627  ...                     0.0           0.0
3         0.32794       0.32794  ...                     0.0           0.0
4         0.52044       0.52044  ...                     0.0           0.0
5         0.02790       0.02790  ...                     0.0           0.0
6         0.03779       0.03779  ...                     0.0           0.0
7         2.80318       2.80318  ...                     0.0           0.0
8         0.00000       0.00000  ...                     0.0           0.0
9         0.00000       0.00000  ...                     0.0           0.0

[10 rows x 3154 columns]

Relative abundances are percentage numbers of the counts. They apply to each taxonomic rank so that adding up the relative abundances per rank should be close to 100%. It may be lower since we removed viruses and unclassified reads.

import numpy as np

We can create a basic sanity check based on above ideas. For each rank individually, the relative abundance should sum up to (maximally) 100 in every sample.

for rank in abundance.columns.unique(level="rank"):
    view = abundance.loc[:, abundance.columns.get_loc_level(rank, level="rank")[0]]
    total = view.sum(axis=1)
    assert ((total < 100.0) | np.isclose(total, 100.0)).all()

How many variables (columns, features) do we actually have per rank?

for rank in abundance.columns.unique(level="rank"):
    print(rank, abundance.columns.get_loc_level(rank, level="rank")[0].sum())

k 3
p 27
c 57
o 92
f 184
g 443
s 1265
t 1083

Since we have the most variables at the species level and because I wouldn’t outright trust MGS’ ability to distinguish strains, we will use the species level for our machine learning tasks. We can always go to a higher taxonomic rank to test performance on more aggregate signals.

species_abundance = abundance.loc[
    :, abundance.columns.get_loc_level("s", level="rank")[0]
].copy()

species_abundance.shape

(800, 1265)

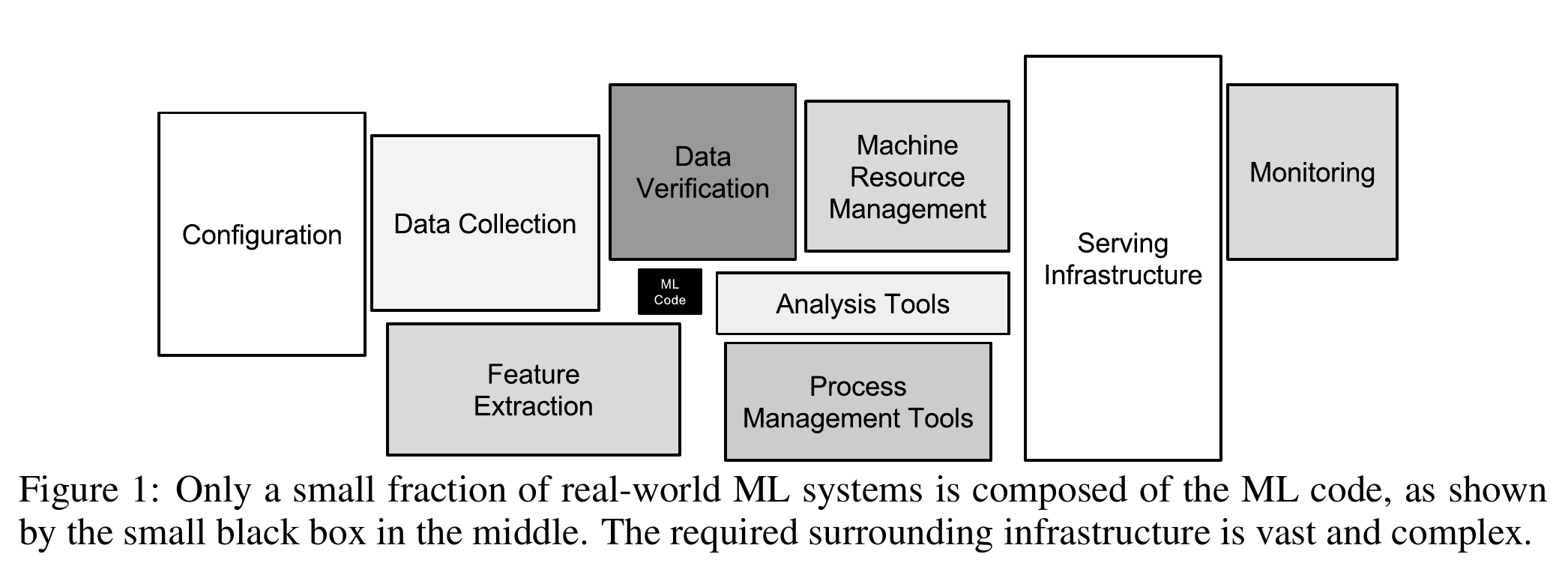
This was a lot of work, you may think, and we haven’t even done any machine learning yet! You are completely right about that feeling. According to a white paper by Google engineers, creating machine learning models is a tiny fraction of the work.

Introduction to Machine Learning

Andrew Ng, a prominent machine learning expert, has defined machine learning as “the science of getting computers to act without being explicitly programmed.” This workshop is meant to give a quick introduction to some of the techniques one can use to build algorithms that meet this criterion. Specifically, we will discuss the following sub-fields within machine learning:

• Dimensionality Reduction (for analyzing and visualizing high-dimensional data sets)
• Clustering (for grouping similar objects in a high dimensional space)
• Classification (for using labeled data to infer labels for unlabeled data)
• Anomaly Detection (for finding outliers in a data set)

Let’s dive in!

Dimensionality Reduction

Our relative abundances data set at the species level has a large number of variables (features in machine learning lingo). We have 1265 features and only 800 samples. Microbiome data are often also quite sparse that means most species are only observed in a small number of samples.

Such “high-dimensional” data sets can be quite hard to work with and reason about, not to mention impossible to visualize. High-dimensional data also pose specific challenges to many machine learning models (see The Curse of Dimensionality). To work around these challenges, it’s often helpful to reduce the number of dimensions required to express a given data set.

One popular way to reduce the dimensionality of a data set is to use a technique called Principal Component Analysis. PCA tries to find a lower dimensional representation of data points by projecting them down into a smaller dimensional space in a way that minimizes loss of information.

To get an intuition about PCA, suppose you have points in two dimensions, and you wish to reduce the dimensionality of your data set to a single dimension. To do so, you could find the center of the points then create a line $L$ with a random orientation that passes through that center. One can then project each point onto $L$ such that an imaginary line between the point and $L$ forms a right angle. Within this “projection”, each 2D point can be represented by just its position along the 1D line $L$, effectively giving us a 1D representation of the point’s position in its original space. Furthermore, we can use the difference between the largest and smallest values of points projected onto $L$ as a measure of the amount of “variance” or “spread” within the data captured by $L$. The greater this spread, the greater the amount of “signal” from the original data set is represented in the projection.

If one were to slowly rotate $L$ and continue measuring the difference between the greatest and smallest values on $L$ at each orientation, one could find the orientation of the projection line that minimizes information loss (maximizes spread). This line of minimal information loss is shown in pink below. Once that line is discovered, we can project all of our points onto that lower-dimensional embedding. See the red points below when the black line is colinear with the pink line:

What makes this kind of dimensionality reduction useful for research? There are two primary uses: (visual) data exploration and data analysis.

Exploratory data visualization with UMAP

Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualization but also for general non-linear dimension reduction. The author Leland McInnes has a recorded presentation about how the method works in detail.

UMAP considers the distances between samples in a particular space (the manifold) and projects those distances to a Cartesian coordinate system with typically two dimensions. That means we need to transform our relative abundances into a square distance matrix that contains the pairwise distance between every sample.

In microbiome analyses, a common metric to compare samples is the Bray-Curtis dissimilarity. It is a $\beta$-diversity measure since we can use it to compare samples from different ecological niches. We use scikit-bio for a fast implementation of this measure.

from skbio.diversity import beta_diversity

bc_dm = beta_diversity(
    metric="braycurtis", counts=species_abundance, ids=observations["sample"]
)

print(bc_dm)

800x800 distance matrix
IDs:
'UT43.2', 'AW107', 'AW108', 'AW110A', 'Zape1', 'Zape2', 'Zape3', 'UT30.3', ...
Data:
[[0.         0.75103997 0.81117371 ... 0.97354678 0.98426476 0.95241561]
 [0.75103997 0.         0.50414618 ... 0.99686836 0.99895874 0.96373897]
 [0.81117371 0.50414618 0.         ... 0.9969896  0.99919453 0.97885096]
 ...
 [0.97354678 0.99686836 0.9969896  ... 0.         0.8080406  0.59635894]
 [0.98426476 0.99895874 0.99919453 ... 0.8080406  0.         0.6525434 ]
 [0.95241561 0.96373897 0.97885096 ... 0.59635894 0.6525434  0.        ]]

Now we are ready to create a lower dimensional projection of this distance matrix.

We would like to take this opportunity to introduce a cool (and in this case useful) feature of Jupyter: interactivity. In order to make the interactivity work as intended, we will define a few functions. One for the UMAP, another to plot the result, and a third to handle the interactivity.

from umap import UMAP

def get_umap_embedding(num):
    """Create a particular projection using a given number of neighbours."""
    result = pd.DataFrame(
        data=UMAP(
            n_neighbors=num, random_state=123456, metric="precomputed", n_components=2
        ).fit_transform(bc_dm.data.copy()),
        columns=["D1", "D2"],
        index=observations.index,
    )
    result[["label", "sample"]] = observations[["label", "sample"]].copy()
    return result

import altair as alt

def plot_umap(df, num):
    """Create an interactive altair chart from a UMAP result."""
    selection = alt.selection_multi(fields=["label"])
    color = alt.condition(
        selection,
        alt.Color("label:N", scale=alt.Scale(scheme="set1"), legend=None),
        alt.value("lightgray"),
    )
    shape = alt.Shape("label", legend=None)

    scatter = (
        alt.Chart(df, title=f"Number of Neighbours = {num}")
        .encode(
            x="D1", y="D2", color=color, shape=shape, tooltip=["sample:N", "label:N"]
        )
        .mark_point(filled=True)
        .interactive()
    )

    legend = (
        alt.Chart(df)
        .encode(
            y=alt.Y("label:N", axis=alt.Axis(orient="right")), color=color, shape=shape
        )
        .mark_point()
        .add_selection(selection)
    )

    return (scatter | legend).configure_view(continuousWidth=800, continuousHeight=600)

from functools import lru_cache

@lru_cache()
def run_umap(num: int):
    embedding = get_umap_embedding(num)
    return plot_umap(embedding, num)

from ipywidgets import interact, widgets

In order to avoid expensive recalculation of results when moving the slider to previous numbers, we use caching.

interact(run_umap, num=widgets.IntSlider(min=5, max=95, step=10, value=15))

The number of neighbours considered is an important parameter for UMAP. Nonetheless, the global structures look very similar. Compare the results to the PCA plot from the paper.

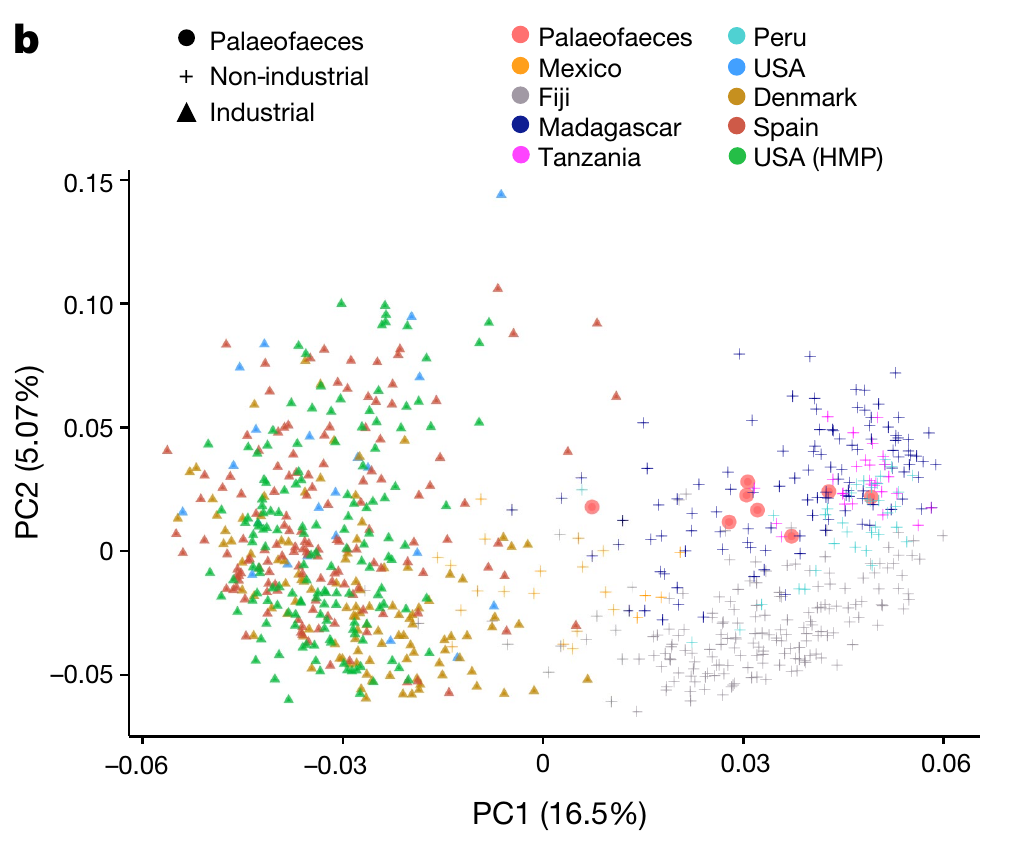
There are very few palaeofaeces and soil samples. We exclude both from further machine learning tasks.

industrial_vs_non_obs = observations[
    observations["label"].isin(["Industrial", "Non-industrial"])
].reset_index(drop=True)

industrial_vs_non_obs.shape

(789, 2)

industrial_vs_non_abn = species_abundance.loc[
    industrial_vs_non_obs.index, :
].reset_index(drop=True)

industrial_vs_non_abn.shape

(789, 1265)

Clustering

Clustering is a powerful machine learning technique and one that often requires some kind of distance metric. The goal of a clustering algorithm is to create some groups of observations, where each group contains similar observations.

There are a variety of methods for clustering vectors, including density-based clustering, hierarchical clustering, and centroid clustering. One of the most intuitive and most commonly used centroid-based methods is K-Means Clustering.

Given a collection of points in a space, K-Means selects K “centroid” points randomly (colored green below), then assigns each non-centroid point to the centroid to which it’s closest. Using these preliminary groupings, the next step is to find the geometric center of each group, using the same technique one would use to find the center of a square. These group centers become the new centroids, and again each point is assigned to the centroid to which it’s closest. This process continues until centroid movement falls below some minimal movement threshold, after which the clustering is complete.

As discussed before, we use PCA to reduce the number of dimensions in our data to two.

from sklearn.decomposition import PCA

pca = PCA(n_components=2).fit(industrial_vs_non_abn)
pca.explained_variance_ratio_

array([0.26181605, 0.1059267 ])

reduced_species = pca.transform(industrial_vs_non_abn)

from sklearn.cluster import KMeans

import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = 16, 12

def plot_kmeans_clusters():
    # Step size of the mesh. Decrease to increase the quality of the VQ.
    h = 0.02  # point in the mesh [x_min, x_max]x[y_min, y_max].

    # Plot the decision boundary. For that, we will assign a color to each
    x_min, x_max = reduced_species[:, 0].min() - 1, reduced_species[:, 0].max() + 1
    y_min, y_max = reduced_species[:, 1].min() - 1, reduced_species[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    # Obtain labels for each point in mesh. Use last trained model.
    Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.figure(1)
    plt.clf()
    plt.imshow(
        Z,
        interpolation="nearest",
        extent=(xx.min(), xx.max(), yy.min(), yy.max()),
        cmap=plt.cm.Paired,
        aspect="auto",
        origin="lower",
    )

    for key, sub in industrial_vs_non_obs.groupby("label", as_index=False, sort=False):
        plt.scatter(
            reduced_species[sub.index, 0],
            reduced_species[sub.index, 1],
            label=key,
        )

    # Plot the centroids as a white X
    centroids = kmeans.cluster_centers_
    plt.scatter(
        centroids[:, 0],
        centroids[:, 1],
        marker="x",
        s=169,
        linewidths=3,
        color="w",
        zorder=10,
    )

    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.xticks(())
    plt.yticks(())
    plt.legend()
    plt.show()

kmeans = KMeans(n_clusters=2, n_init=16, random_state=123456).fit(reduced_species)

plot_kmeans_clusters()

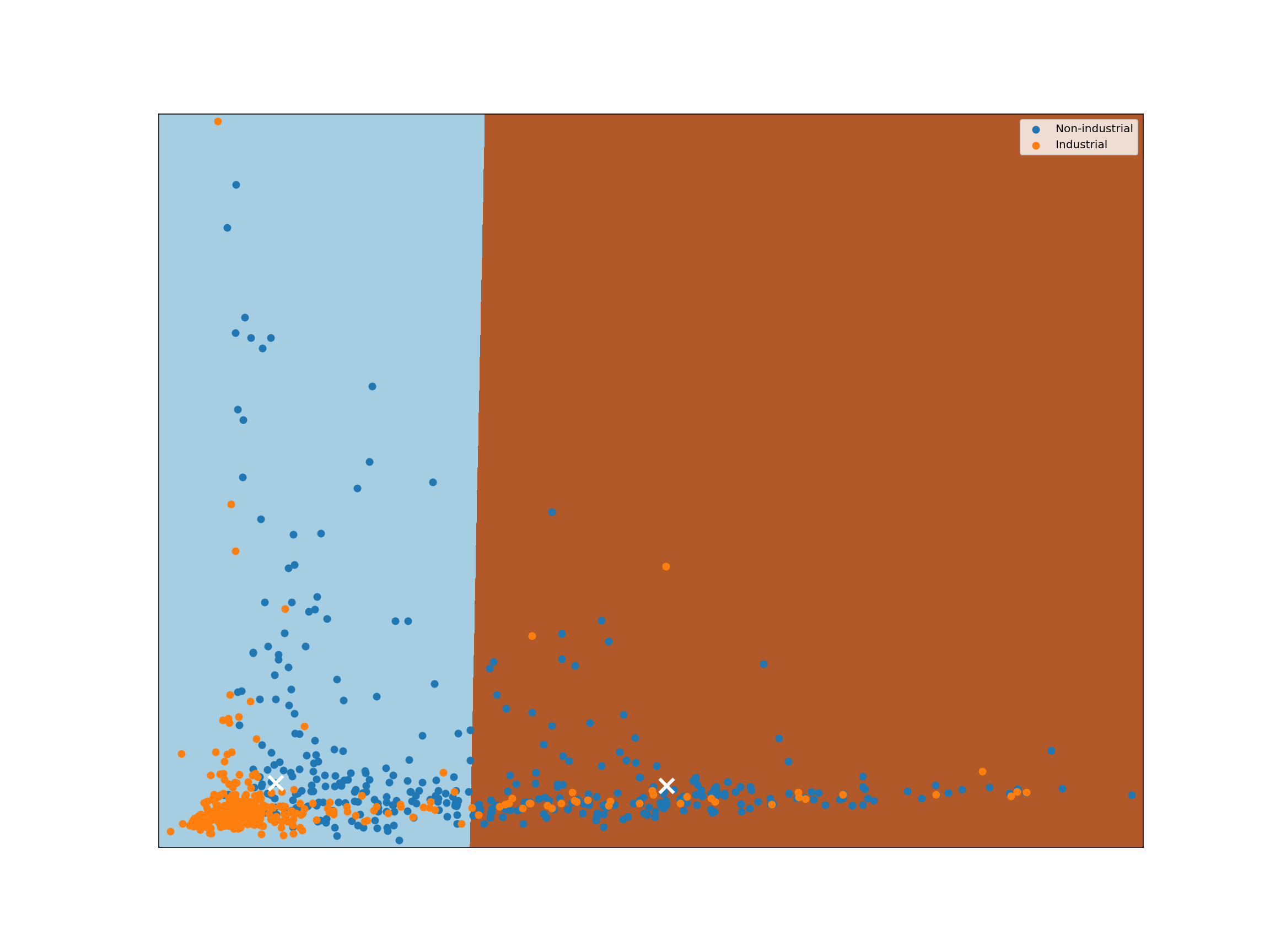
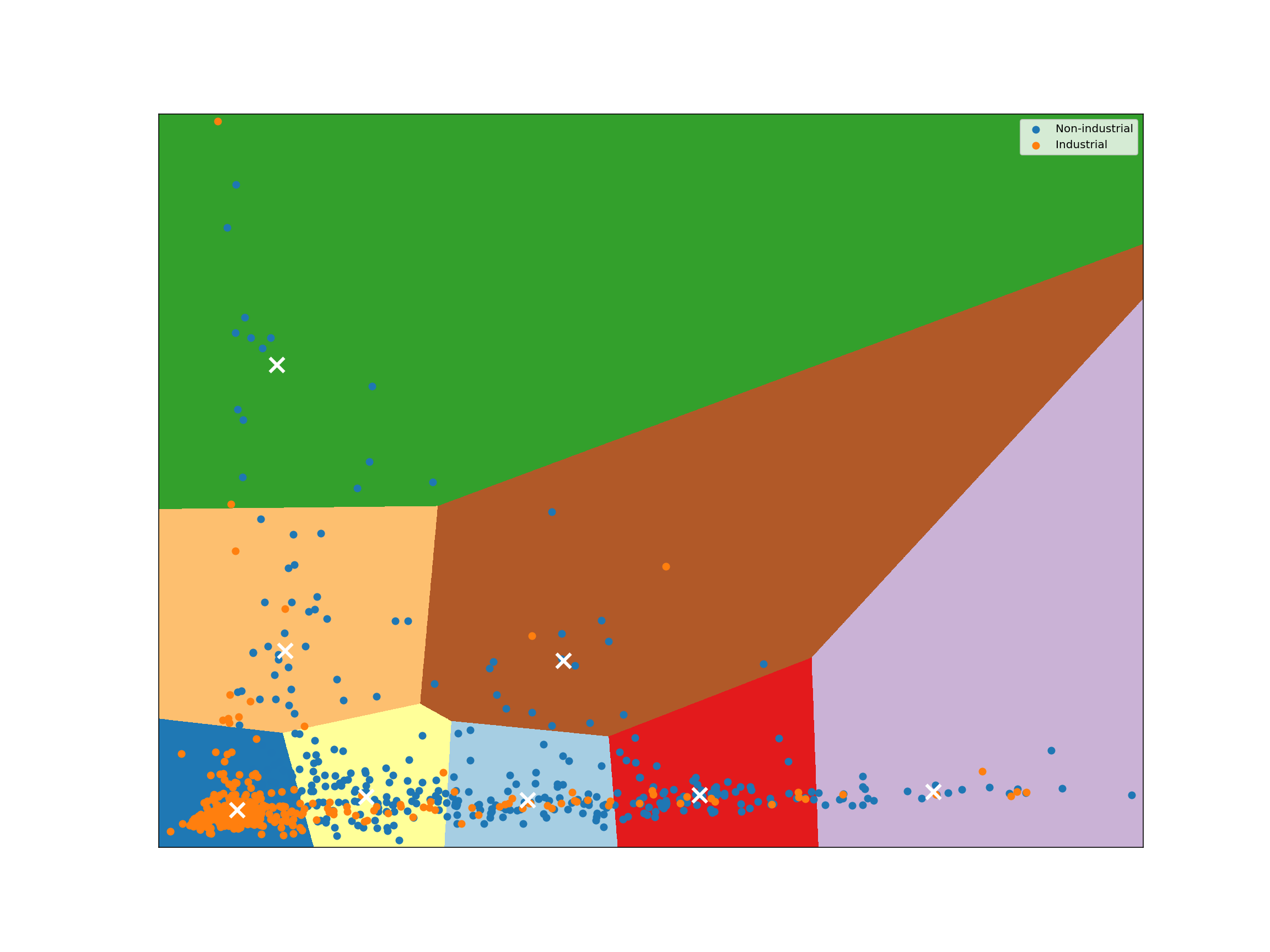
kmeans = KMeans(n_clusters=8, n_init=16, random_state=123456).fit(reduced_species)

plot_kmeans_clusters()

Classification

The goal of a classification task is to predict whether a given observation in a data set possesses some particular property or attribute. To make these predictions, we measure the attributes of several labeled data observations, then compare unknown observations to those measurements.

In our data set we have microbiome samples labeled either as ‘industrial’ or ‘non-industrial’. Scikit-learn can help us to split out data into a training set and a testing set.

K-Nearest neighbors classifiers

With a $K$-nearest neighbors classifier, we start with a labeled data set. We then add new, unlabeled observations to the data. For each, we consult the $K$ labeled observations to which the unlabeled observation is closest, where $K$ is an odd integer we use for all classifications. We then find the most common label among those $K$ observations (the “$K$-nearest neighbors”) and give the new observation that label.

The following diagram shows this scenario. Our new observation (represented by the question mark) has some points near it that are labeled with a triangle or star. Suppose we have chosen to use 3 for our value of $K$. In that case, we consult the 3 nearest labeled points near the question mark. Those 3 nearest neighbors have labels: star, triangle, triangle. Using a majority vote, we give the question mark a triangle label.

Examining the plot above, we can see that if $K$ were set to 1, we would classify the question mark as a star, but if K is 3 or 5, we would classify the question mark as a triangle. That is to say, $K$ is an important parameter in a $K$-nearest neighbors classifier.

Let’s see how we can use our labeled microbiome samples for classification.

With scikit-learn’s convenience function, we split our data into a training set and a test set. By default the size is approximately 3:1.

from sklearn.model_selection import train_test_split

train_abundance, test_abundance, train_label, test_label = train_test_split(
    reduced_species, industrial_vs_non_obs["label"]
)

np.unique(train_label, return_counts=True)

(array(['Industrial', 'Non-industrial'], dtype=object), array([317, 274]))

np.unique(test_label, return_counts=True)

(array(['Industrial', 'Non-industrial'], dtype=object), array([101,  97]))

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import matthews_corrcoef

@lru_cache
def run_knn(num):
    knn_clf = KNeighborsClassifier(num).fit(train_abundance, train_label)
    return matthews_corrcoef(test_label, knn_clf.predict(test_abundance))

interact(run_knn, num=widgets.IntSlider(min=1, max=9, step=2, value=3))

Measure performance

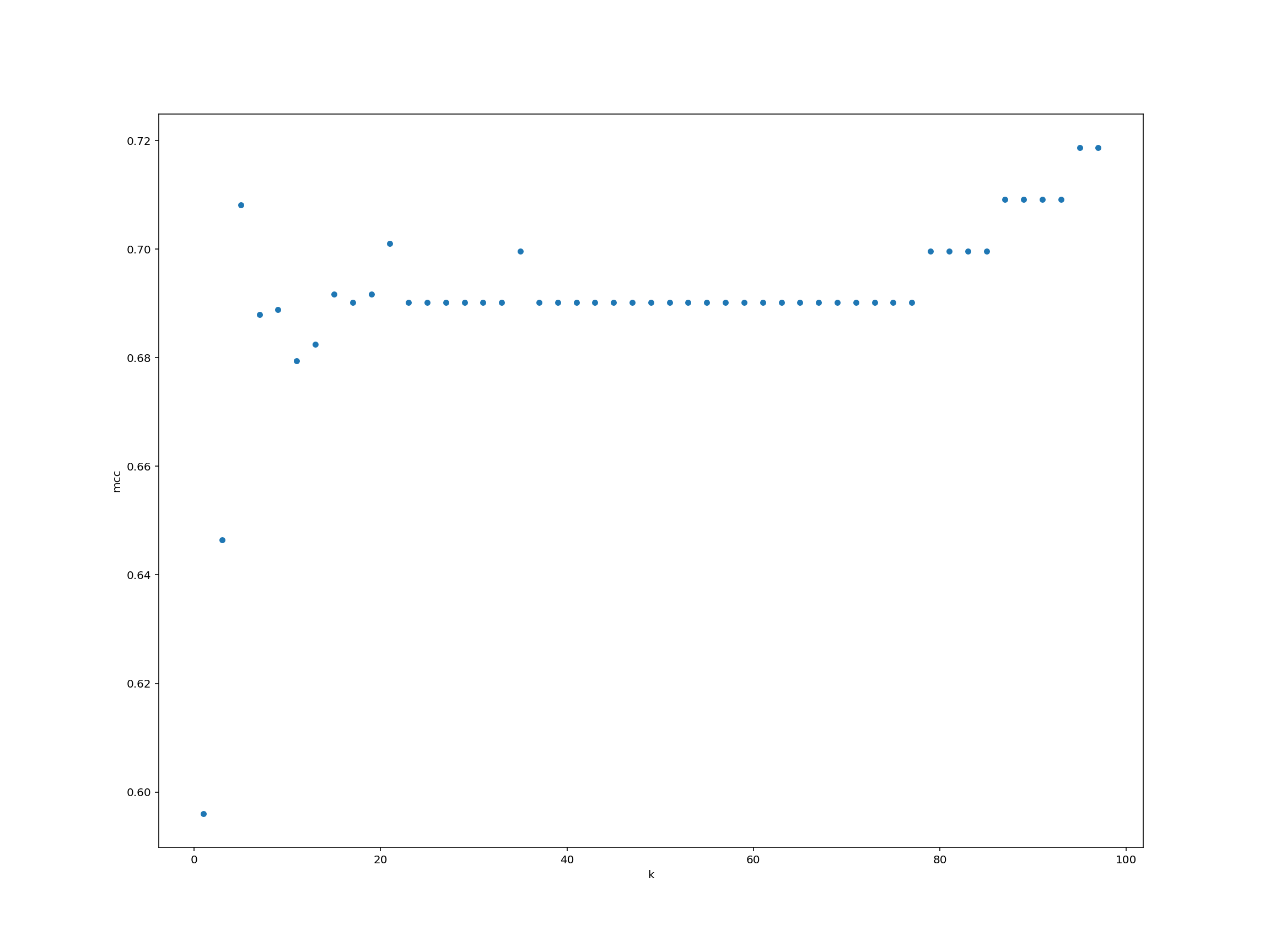
Can you systematically measure the classifier model performance (as measured by Matthews’ correlation coefficient) for a wide range of $K$-values? Plot the results using any method that we have learnt.

Solution

We create a data frame for storing the $K$-values and performance.

performance = pd.DataFrame({"k": list(range(1, 99, 2))})

performance["mcc"] = performance["k"].map(run_knn)

performance.plot.scatter("k", "mcc")

For each observation we pass as input to knn_clf.predict(), the function returns a label (either 0 or 1). Just like that, we’ve trained a machine learning classifier and classified some test data!

The classification example above shows how we can classify just a single point in space, but suppose we want to analyze the way a classifier would classify each possible point in some space. To do so, we can transform our space into a grid of units, then classify each point in that grid. Analyzing a space in this way is known as identifying a classifier’s decision boundary, because this analysis shows one the boundaries between different classification outcomes in the space. This kind of analysis is very helpful in training machine learning models, because studying a classifier’s decision boundary can help one see how to improve the classifier.

Let’s take a look at the decision boundary of our classifier:

def plot_decision_boundary(clf, X, labels, h=0.1):
    # Plot the decision boundary. For that, we will assign a color to each
    # point in the mesh [x_min, x_max]x[y_min, y_max].
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.RdBu, alpha=0.8)

    # Plot also the training points
    for key, sub in labels.groupby("label", as_index=False, sort=False):
        plt.scatter(X[sub.index, 0], X[sub.index, 1], edgecolor="black", label=key)

    plt.legend(loc="best")
    plt.show()

knn_clf = KNeighborsClassifier(5).fit(train_abundance, train_label)

plot_decision_boundary(
    knn_clf,
    train_abundance,
    pd.DataFrame({"label": train_label}).reset_index(drop=True),
)

For each pixel in the plot above, we retrieve the $K$ closest points with known labels. We then use a majority vote of those labels to assign the label of the pixel. This is exactly analogous to predicting a label for an unlabeled point. In both cases, we take a majority vote of the $K$ closest points with known labels. Working in this way, we can use labeled data to classify unlabeled data. That’s all there is to $K$-nearest neighbors classification!

It’s worth noting that $K$-nearest neighbors is only one of many popular classification algorithms. From a high-level point of view, each classification algorithm works in a similar way. Each requires a certain number of observations with known labels and each uses those labeled observations to classify unlabeled observations. However, different classification algorithms use different logic to assign a label to new observations which means different classification algorithms have very different decision boundaries.

In the chart below, each row plots the decision boundaries several classifiers give the same data set. Notice how some classifiers work better with certain data shapes.

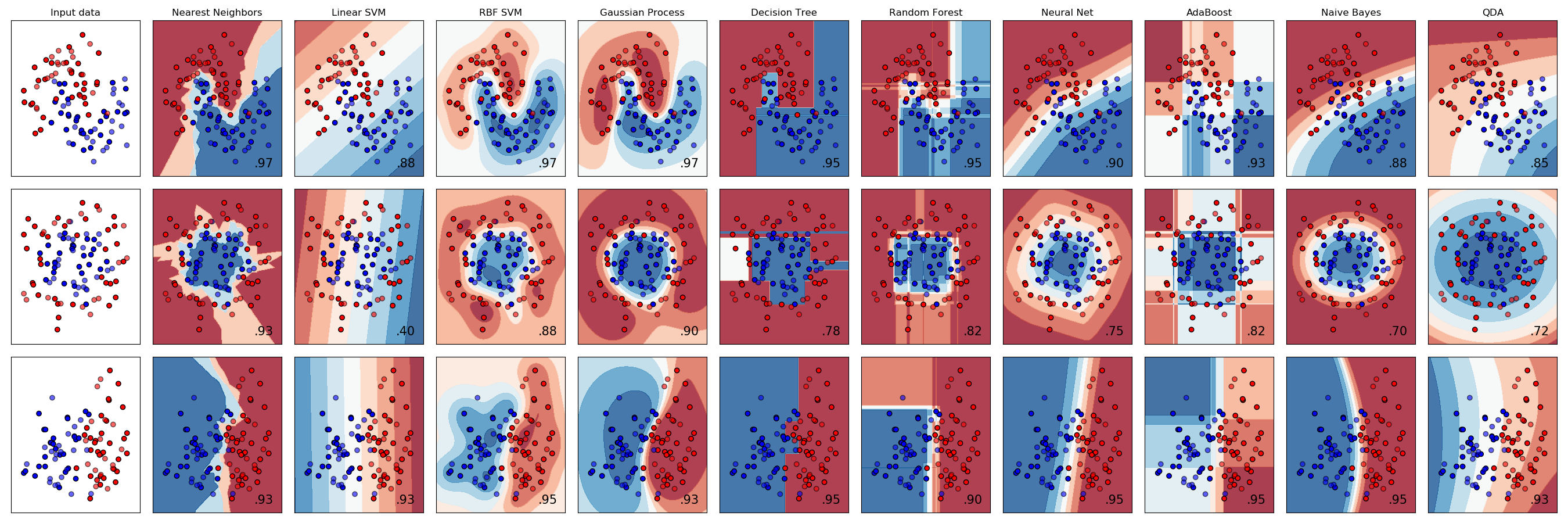
For an intuitive introduction to many of these classifiers, including Support Vector Machines, Decision Trees, Neural Networks, and Naive Bayes classifiers, see Luis Serrano’s introduction to machine learning video discussed in the Going Further section below.

Anomaly Detection

Anomaly detection refers to the identification of anomalies, or outliers, in data sets. While detecting anomalies in a single dimension can be quite simple, finding anomalies in high-dimensional space is a difficult problem.

One technique for classifying anomalies in high-dimensional data sets is an Isolation Forest. An Isolation Forest identifies outliers in a data set by randomly dividing a space until each point is isolated from each other. After repeating this procedure several times, the Isolation Forest identifies points that are more quickly isolated from other points as outliers.

This illustration demonstrates the method by which these outliers are quickly identified. Isolated points are colored green and labeled with the iteration on which they were isolated. If you repeat the procedure several times, you’ll see the outlier is consistently isolated quickly, which allows the Isolation Forest to identify that point as an outlier.

If we run the simulation above a number of times, we should see the outlier point is consistently isolated quickly, while it usually takes more iterations to isolate the other points. This is the chief intuition behind the Isolation Forests outlier classification strategy. Outliers are isolated quickly because they are farther from other points in the data set.

Let’s try this on our microbiome samples.

from sklearn.ensemble import IsolationForest

isolation_clf = IsolationForest(random_state=123456, n_jobs=-1).fit(train_abundance)

def plot_iforest_decision_boundary(clf, X, test_X, test_result, margin=6, mesh=0.5):
    """
    Create and display the decision boundary for an isolation forest.
    """
    # get the x and y grid domains
    x_domain = [X[:, 0].min() - margin, X[:, 0].max() + margin]
    y_domain = [X[:, 1].min() - margin, X[:, 1].max() + margin]
    # get a list of values from min to max, counting by `mesh`
    x_range = np.arange(x_domain[0], x_domain[1], mesh)
    y_range = np.arange(y_domain[0], y_domain[1], mesh)
    # create the data with which to color the background grid
    xx, yy = np.meshgrid(x_range, y_range)
    # classify each unit of the grid
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    # reshape Z into a 2D grid
    Z = Z.reshape(xx.shape)
    # fill in the grid values
    plt.contourf(xx, yy, Z, cmap=plt.cm.YlGn)
    # add the training points
    plt.scatter(
        X[:, 0],
        X[:, 1],
        c="green",
        edgecolors="black",
        alpha=0.4,
        label="training observation",
    )
    inliers = test_X[test_result == 1, :]
    outliers = test_X[test_result == -1, :]
    # plot the inliers and outliers
    if inliers.shape[0] > 0:
        plt.scatter(
            inliers[:, 0],
            inliers[:, 1],
            c="white",
            edgecolors="black",
            label="non-outlier",
        )
    if outliers.shape[0] > 0:
        plt.scatter(
            outliers[:, 0], outliers[:, 1], c="red", edgecolors="black", label="outlier"
        )
    # add a legend to the plot
    plt.legend(loc="best")
    plt.show()

plot_iforest_decision_boundary(
    isolation_clf, train_abundance, test_abundance, isolation_clf.predict(test_abundance)
)

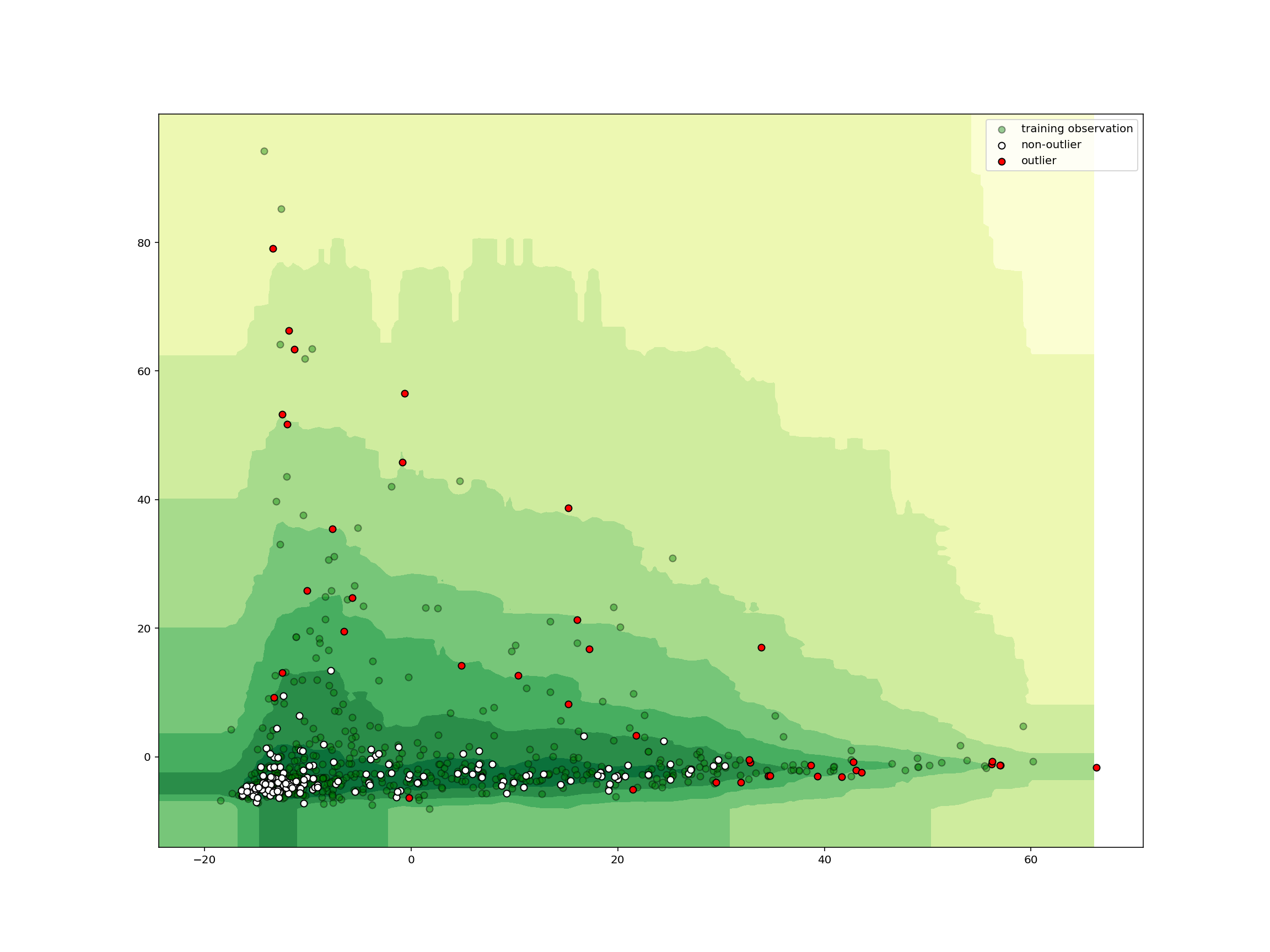
We see that any samples outside the central area is classified as an outlier. In just a few lines of code, we can create, train, and deploy a machine learning model for detecting outliers in high-dimensional data!

Removed samples

In the original study, some samples were removed. Can our classifier detect them as outliers?

Prepare data

As before we load the data from the spreadsheet and tidy it up.

removed = pd.read_excel(
    "data/41586_2021_3532_MOESM6_ESM.xlsx", sheet_name="Tab2-MetaPhlAn2_removed_samples"
)

removed

                                            Unnamed: 0    TS929A  ...    AW113    AW116
0                                           k__Archaea  44.35047  ...  0.47962  0.02775
1                          k__Archaea|p__Euryarchaeota  44.35047  ...  0.47962  0.02775
2       k__Archaea|p__Euryarchaeota|c__Methanobacteria  44.35047  ...  0.47962  0.02775
3    k__Archaea|p__Euryarchaeota|c__Methanobacteria...  44.35047  ...  0.47962  0.02775
4    k__Archaea|p__Euryarchaeota|c__Methanobacteria...  44.35047  ...  0.47962  0.02775
..                                                 ...       ...  ...      ...      ...
729  k__Viruses|p__Viruses_noname|c__Viruses_noname...   0.00000  ...  0.46174  0.00000
730  k__Viruses|p__Viruses_noname|c__Viruses_noname...  12.62477  ...  0.00000  0.00000
731  k__Viruses|p__Viruses_noname|c__Viruses_noname...  12.62477  ...  0.00000  0.00000
732  k__Viruses|p__Viruses_noname|c__Viruses_noname...  12.62477  ...  0.00000  0.00000
733  k__Viruses|p__Viruses_noname|c__Viruses_noname...  12.62477  ...  0.00000  0.00000

[734 rows x 8 columns]

def transform_removed_taxonomic_rank(df: pd.DataFrame) -> pd.DataFrame:
    result = df.rename(columns={"Unnamed: 0": "taxonomy"})
    lineage = result["taxonomy"].str.split("|")
    result["kingdom"] = (
        lineage.map(lambda element: element[0])
        .str.split("__", n=1, expand=True)
        .iloc[:, -1]
    )
    result[["rank", "taxonomy"]] = lineage.map(lambda element: element[-1]).str.split(
        "__", n=1, expand=True
    )
    return result

intermediate = transform_removed_taxonomic_rank(removed)

intermediate.head(10)

                                  taxonomy    TS929A  TS889  ...    AW116  kingdom  rank
0                                  Archaea  44.35047    0.0  ...  0.02775  Archaea     k
1                            Euryarchaeota  44.35047    0.0  ...  0.02775  Archaea     p
2                          Methanobacteria  44.35047    0.0  ...  0.02775  Archaea     c
3                       Methanobacteriales  44.35047    0.0  ...  0.02775  Archaea     o
4                      Methanobacteriaceae  44.35047    0.0  ...  0.02775  Archaea     f
5                       Methanobrevibacter  44.35047    0.0  ...  0.02741  Archaea     g
6               Methanobrevibacter_smithii   0.00000    0.0  ...  0.01242  Archaea     s
7  Methanobrevibacter_smithii_unclassified   0.00000    0.0  ...  0.01242  Archaea     t
8          Methanobrevibacter_unclassified  44.35047    0.0  ...  0.01499  Archaea     s
9                           Methanosphaera   0.00000    0.0  ...  0.00035  Archaea     g

[10 rows x 10 columns]

intermediate.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 734 entries, 0 to 733
Data columns (total 10 columns):
 #   Column    Non-Null Count  Dtype  
---  ------    --------------  -----  
 0   taxonomy  734 non-null    object 
 1   TS929A    734 non-null    float64
 2   TS889     734 non-null    float64
 3   TS895     734 non-null    float64
 4   UT2.12    734 non-null    float64
 5   UT3.6     734 non-null    float64
 6   AW113     734 non-null    float64
 7   AW116     734 non-null    float64
 8   kingdom   734 non-null    object 
 9   rank      734 non-null    object 
dtypes: float64(7), object(3)
memory usage: 57.5+ KB

intermediate[["taxonomy", "kingdom", "rank"]].describe()

              taxonomy   kingdom rank
count              734       734  734
unique             731         4    8
top     Viruses_noname  Bacteria    s
freq                 3       675  258

intermediate["kingdom"].value_counts()

Bacteria     675
Eukaryota     27
Viruses       20
Archaea       12
Name: kingdom, dtype: int64

intermediate["rank"].value_counts()

s    258
t    204
g    129
f     75
o     33
c     21
p     10
k      4
Name: rank, dtype: int64

removed_abundance = (
    intermediate.query("kingdom != 'Viruses'")
    .set_index(["kingdom", "rank", "taxonomy"])
    .T.reset_index(drop=True)
)

removed_abundance

kingdom    Archaea                ...           Eukaryota              
rank             k             p  ...                   s             t
taxonomy   Archaea Euryarchaeota  ... Sordaria_macrospora GCA_000182805
0         44.35047      44.35047  ...             0.00000       0.00000
1          0.00000       0.00000  ...             0.00000       0.00000
2          0.52994       0.52994  ...             0.00000       0.00000
3          0.00666       0.00666  ...             0.00000       0.00000
4          0.03470       0.03470  ...             0.00000       0.00000
5          0.47962       0.47962  ...             0.96528       0.96528
6          0.02775       0.02775  ...             0.55437       0.55437

[7 rows x 714 columns]

Now that we have the data in a tidy format, we should include missing variables before reducing the whole set again to two dimensions by PCA.

removed_species = removed_abundance.loc[
    :, removed_abundance.columns.get_loc_level("s", level="rank")[0]
].copy()

removed_species.shape

(7, 254)

industrial_vs_non_abn.shape

(789, 1265)

removed_species = removed_species.reindex(
    columns=removed_species.columns.union(industrial_vs_non_abn.columns), fill_value=0
)

removed_species

kingdom                     Archaea  ...       Eukaryota
rank                              s  ...               s
taxonomy Halobacterium_unclassified  ... Ustilago_maydis
0                                 0  ...               0
1                                 0  ...               0
2                                 0  ...               0
3                                 0  ...               0
4                                 0  ...               0
5                                 0  ...               0
6                                 0  ...               0

[7 rows x 1229 columns]

reduced_removed = PCA(n_components=2).fit_transform(removed_abundance.values)

reduced_removed.shape

(7, 2)

plot_iforest_decision_boundary(
    isolation_clf,
    reduced_species,
    reduced_removed,
    isolation_clf.predict(reduced_removed),
)

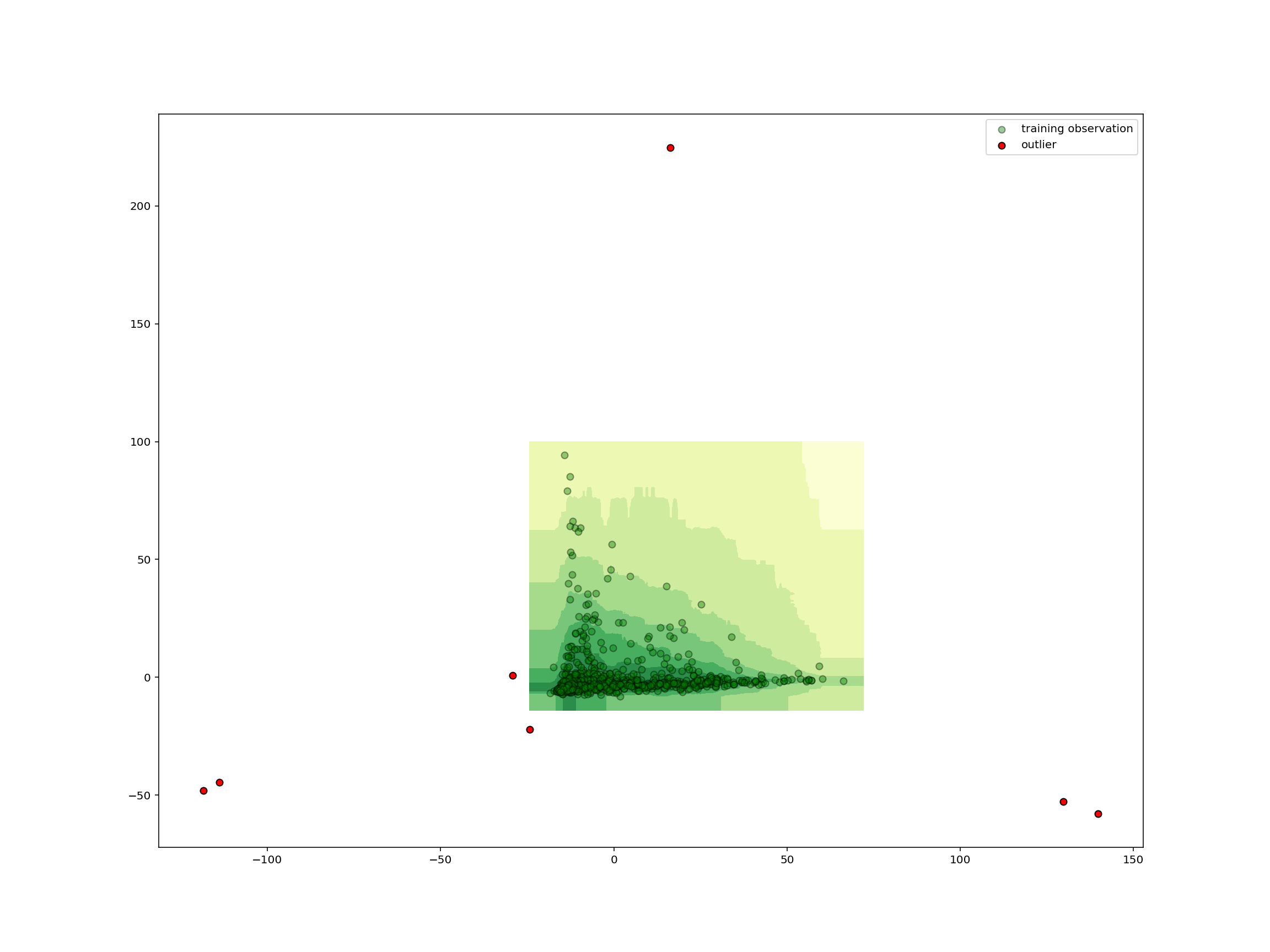
As we could have expected from the small number of shared species, the removed samples are far from all the other samples and thus all outliers.

Going Further

The snippets above are meant only to give a brief introduction to some of the most popular techniques in machine learning so you can decide whether this kind of analysis might be useful in your research. If it seems like machine learning will be important in your work, you may want to check out some of the resources listed below (arranged roughly from least to most technical):

• A Friendly Introduction to Machine Learning

  In this 30 minute video, Luis Serrano (head of machine learning at Udacity) offers intuitive, user-friendly introductions to the mechanics that drive a number of machine learning models, including Naive Bayes, Decision Tree, Logistic Regression, Neural Network, and Support Vector Machine classifiers. This video is a great place to start for those looking for quick intuitions about the ways these algorithms work.

• Hands-On Machine Learning with Scikit-Learn and TensorFlow (OREILLY)

  This OREILLY book offers a great high-level introduction to machine learning with Python. Aurélien Géron guides readers through ways one can use scikit-learn and other popular libraries to build machine learning models in Python. This is a great choice for those who just want to get work done, without necessarily unlocking the insights that would allow one to build models from scratch.

• Machine Learning Cheatsheets

  This collection of “cheat sheets” gives concise overviews of the api’s and models behind many of the most prominent packages and concepts in machine learning and its allied fields, including different neural network architectures, numerical optimization techniques, algorithms appropriate for different tasks, scikit-learn, pandas, scikit-learn, scipy, ggpot2, dplyr and tidyr, big O notation, and a number of other topics. Recently identified as the “most popular” article on machine learning in Medium.

• Mining of Massive Datasets

  This Stanford University course and digital publication offer introductions to a wide array of subtopics in machine learning. The authors focus on helping readers gain an intuitive understanding of how machine learning models work. One of the most lucid and concise treatments of machine learning available on the web.

• Convolutional Neural Networks for Visual Recognition

  This Stanford University course offers a spectacular introduction to Convolutional Neural Networks, the cornerstone of modern machine learning in the domain of computer vision. If your work involves images or video materials, and you’d like to apply machine learning techniques to your data, this course will help you get up and running with state-of-the-art techniques in convnets.

• Machine Learning (Andrew Ng, Coursera)

  Andrew Ng’s Coursera course on machine learning will help you master many of the fundamentals involved in modern machine learning. Professor Ng will guide you through a great deal of the math involved in contemporary machine learning, starting with simple linear classifiers and building up into complex neural network architectures. This class is ideal for those who like to understand the math behind the models they use.

Key Points

• Preparing data in the right format is often the hardest task.

• Machine learning provides methods for tasks such as dimensionality reduction, clustering, classification, and anomaly detection.

• Having good visualizations is crucial for interpretation.

Afternoon Break

Overview

Teaching: 0 min
Exercises: 0 min

Questions

Objectives

Key Points

Machine Learning (continued)

Overview

Teaching: 0 min
Exercises: 0 min

Questions

Objectives

Please see the previous episode for the content.

Key Points

Wrap-up and Outlook

Overview

Teaching: 0 min
Exercises: 0 min

Questions

Objectives

Getting help:

• Stackoverflow: dominant Q&A site for everything programming related (typically would end up here after a Google search)
• Biostars: Q&A site for bioinformatics related questions
• If you really get stuck, ask questions in the course’s MS Team channel!

Further course materials (in the same style of the course):

• Software carpentry: collection of official and community contributed course materials on learning programming languages (also R and Matlab) and related computational tools
• Data carpentry: huge collection of official and community contributed course materials on data science & engineering (also covering Biology a bit)

Good coding practices and advise:

• Ten simple rules for biologists learning to program: excellent advise for newcomers
• Good Computational Biology practices: (somewhat opinionated) advised on good practices in computational biology (work in progress …)

Python libraries relevant for biotech (not covered in the course):

• Biopython: work with biological sequences
• Pydna: molecular cloning, PCR simulation, primer design, …
• scikit-image: image processing and computer vision (counting colonies, cells, …)
• auto-sklearn: auto-ML of scikit-learn
• opentrons: program opentrons liquid handlers using Python
• cobrapy: work with metabolic models
• cameo: use metabolic models for cell factory design

Popular visualization and dashboard libraries (not covered in the course):

• plotly: plotting tool with interfaces for many different programming languages (including Python, R, Matlab, …) producing interactive visualizations
• dash: create dashboards similar to Tableau, Spotfire, Microsoft Power BI etc.using Python code (similar to R shiny; uses plotly for the charts)
• Bokeh: interactive visualizations with sliders and buttons etc.
• Seaborn: good statistical visualization with error bars, violin plots etc. (written on top of matplotlib)

Finding more packages:

• The Python Package Index

Key Points